基本不等式,在高考数学中一般指代数-几何均值不等式(Inequality of Arithmetic and Geometric Means, AM-GM Inequality),是高中数学的重要不等式之一.在高中主要研究二元和三元情况.
前一节我们提到过一个重要的不等式:对于任意 a,b∈R,有 a2+b2≥2ab,当且仅当 a=b 时等号成立.
特殊地,将 a,b 分别替换为 a,b,其中 a,b>0,则可以推出基本不等式.
对于任意 a,b∈R+,有
ab≤2a+b,
当且仅当 a=b 时等号成立.
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.
要证
ab≤2a+b,
只需证
2ab≤a+b,
只需证
a+b−2ab≥0,
只需证
(a−b)2≥0.
上式显然成立,当且仅当 a=b 时,上式中的等号成立.因此,原不等式成立.证毕.
这种「要证……只需证……」的写法常用于考试中的证明题.
对于任意 a,b<0,有
a+b≤−2ab,
当且仅当 a=b 时等号成立.
证明:
(−a)+(−b)−(a+b)a+b≥2(−a)(−b),≥2ab,≤−2ab,
当且仅当 −a=−b,即 a=b 时等号成立.证毕.
对于任意 n 个正实数 a1,a2,…,an,有
n∑i=1nai≥n∏i=1nai,
当且仅当 a1=a2=⋯=an 时等号成立.
在高中,常用基本不等式的三元形式:对于任意 a,b,c∈R+,有
3a+b+c≥3abc,
当且仅当 a=b=c 时等号成立.
-
ab≤4(a+b)2,其中 a,b∈R,当且仅当 a=b 时等号成立.
-
x+x1≥2,其中 x=0,当且仅当 x=±1 时等号成立.
-
ab+ba≥2,其中 a,b∈R 满足 ab=0,当且仅当 a=±b 时等号成立.
-
ax+xb≥2ab,其中 a,b∈R 为常数,x=0,当且仅当 x=±ab 时等号成立.
-
a2+b2+c2≥ab+bc+ca,其中 a,b,c∈R,当且仅当 a=b=c 时等号成立.证明:两边乘 2 后凑成三个完全平方.
对于任意 a,b>0,有
a1+b12≤ab≤2a+b≤2a2+b2,
当且仅当 a=b 时四个式子相等.
上述不等式称为均值不等式(RMP-AM-GM-HM Inequality, or Mean Inequality Chain).
用自然语言叙述为:调和平均数 ≤ 几何平均数 ≤ 算术平均数 ≤ 平方平均数(也称均方根).简记为:「调几算平」.
第一个不等号:
a+ba+b1a+b2aba1+b12≥2ab≤2ab1≤ab≤ab
第三个不等号:
a2+b22a2+2b22a2+b22a2+b2≥2ab≥(a+b)2≥4(a+b)2≥2a+b
证毕.
在解题的过程中,我们常常需要求 ax±xb 的最值,且限制了 x 的范围,使得无法直接应用基本不等式.因此我们需要熟知下面这两种函数的性质.有关函数的基本知识见 [?] 节.
「对勾函数」 指的是形如 y=ax+xb(a,b>0)的一类函数,其
- 位于第一、三象限;
- 分别在第一、三象限有一个极小值点和一个极大值点(通过基本不等式求出);
- 渐近线为 x=0 和 y=ax;
- 是一个奇函数.
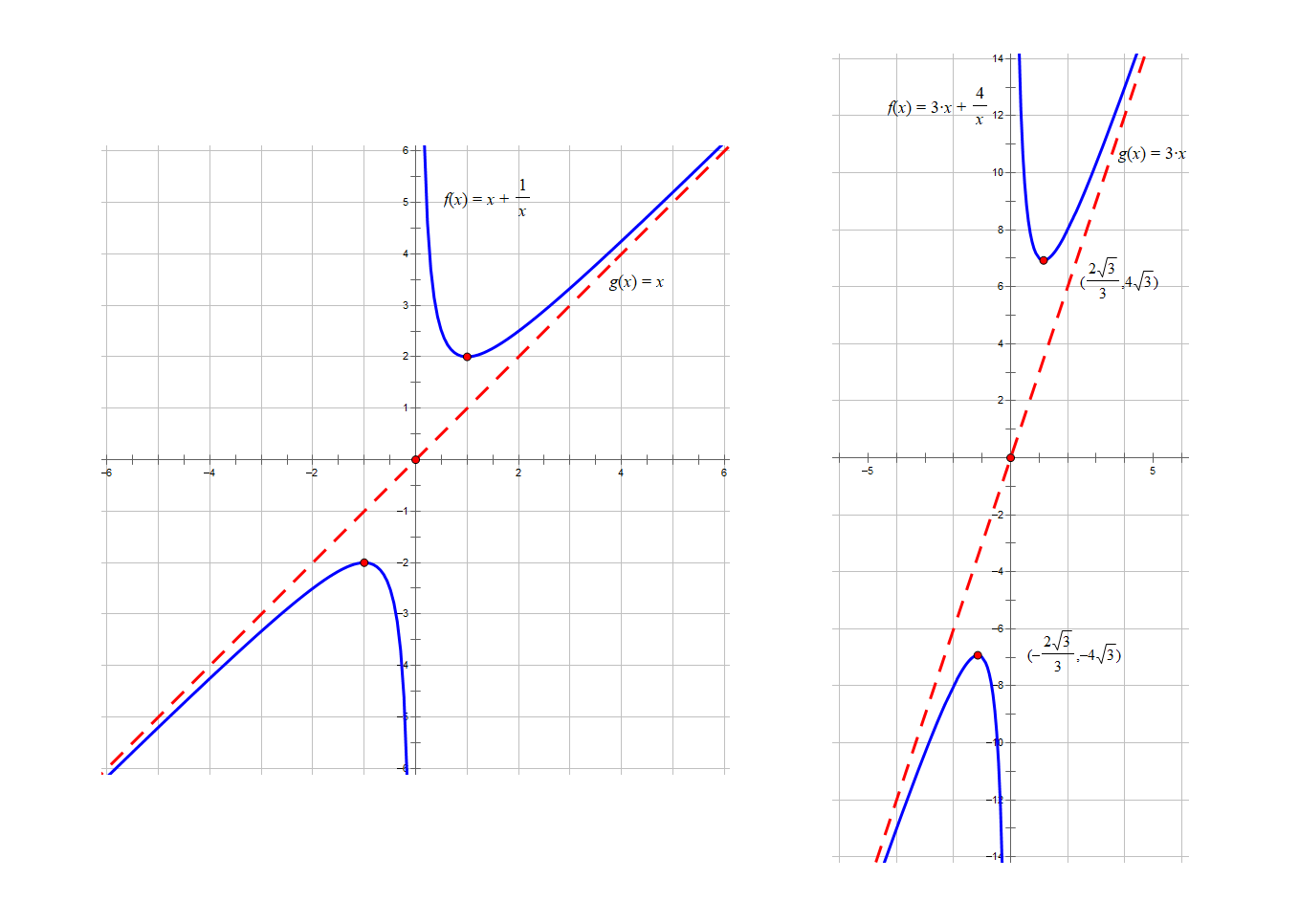
y=x+x1 和 y=3x+x4 图象分别如下图所示:
「飘带函数」 指的是形如 y=ax−xb(a,b>0)的一类函数,其
- 在 (−∞,0) 和 (0,+∞) 上分别单调递增;
- 在 x 轴正、负半轴上分别有一个零点;
- 渐近线为 x=0 和 y=ax;
- 是一个奇函数.
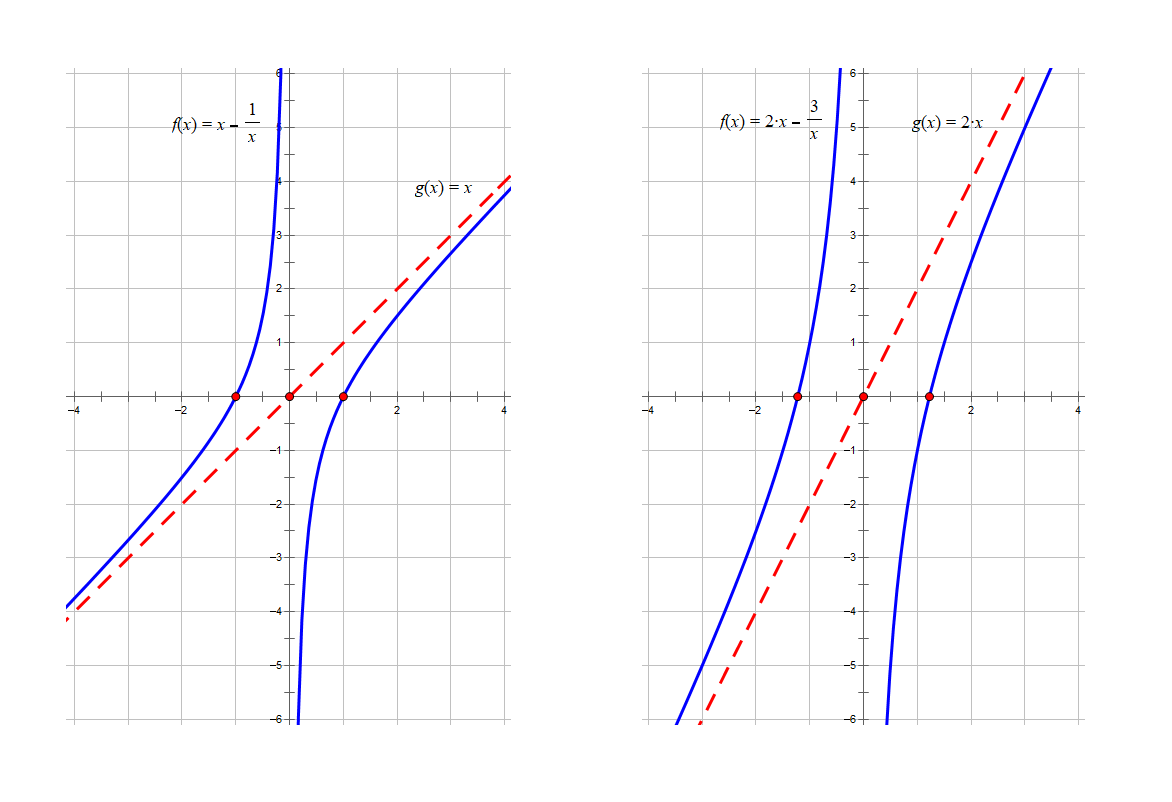
y=x−x1 和 y=2x−x3 图象分别如下图所示:
我们也可以画出其他类似函数的图象,如:
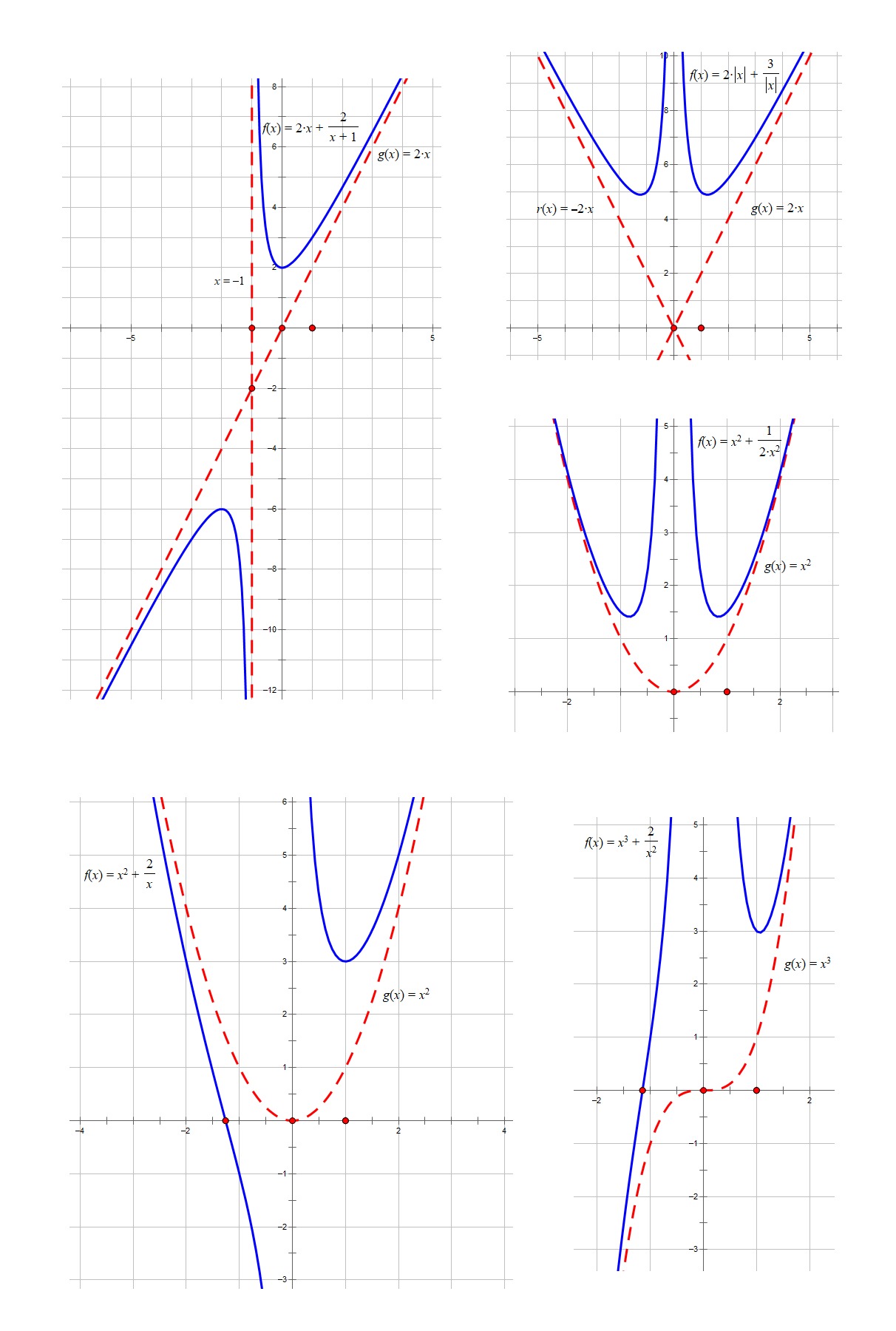
上面这些函数的大致图像可以通过 平移、求极限(渐近线)、研究奇偶性、研究单调性、研究凹凸性等方法画出.
(多选题) 若 x,y 满足 x2+y2−xy=1,则( )
- A. x+y≤1
- B. x+y≥−2
- C. x2+y2≤2
- D. x2+y2≥1
先求 x+y 的范围.由所给等式和基本不等式得
(x+y)2=1+3xy≤1+3⋅4(x+y)2,解得 −2≤x+y≤2,当且仅当 x=y=−1 时 x+y=−2,当且仅当 x=y=1 时 x+y=2.所以 A 错误,B 正确.
再求 x2+y2 的范围.注意到其与平方平均数有关,由 xy≤2x2+y2 得
x2+y2=1+xy≤1+2x2+y2,解得 x2+y2≤2,当且仅当 x=y=±1 时等号成立.所以 C 正确.
*对于 D,对所给等式配方得 (x−2y)2+(23y)2=1,使用 三角换元法,设
x−2y=cosθ,23y=sinθ,θ∈R,即
x=cosθ+33sinθ,y=323sinθ,因此 x2+y2=cos2θ+35sin2θ+323sinθcosθ=34+32sin(2θ−6π)∈[32,2].所以 D 错误.(有关三角函数的知识见 [?] 节.)
故选 BC.
对于 D,也可以采用 特殊值法,代入 x=33,y=−33,则 x2+y2−xy=1,但 x2+y2=32<1,不符合选项,所以 D 错误.
对于 x,y>0:
- 如果积 xy 为定值,则 x+y 有最小值 2xy,当且仅当 x=y 时取到.
- 如果和 x+y 为定值,则 xy 有最大值 4(x+y)2,当且仅当 x=y 时取到.
应用条件简记为 「一正二定三相等」 或 「正定等」.
之所以把常值代换法放在第一个,是因为它太常考了.最常考的形式是:
- 若 a,b,c,m,n,x,y>0,其中 a,b,c,m,n 是常数,且 ax+by=c,则
xm+yn=c1(ax+by)(xm+yn)=c1(am+bn+xbmy+yanx)≥c1(am+bn+2abmn)=c1(am+bn)2.
- 若 a,b,c,m,n,x,y>0,其中 a,b,c,m,n 是常数,且 xa+yb=c,则
mx+ny=c1(mx+ny)(xa+yb)=c1(am+bn+xany+ybmx)≥c1(am+bn+2abmn)=c1(am+bn)2.
上面的公式可以不用记住,记住使用 常值代换法 的过程即可.
已知 a,b>0,a+2b=2,求 2a+bab 的最大值.
其实这道例题节选自一道解析几何题目的一个步骤,可见打好基础的重要性.
首先取倒数得
ab2a+b=a1+b2=21(a+2b)(a1+b2)=21(1+4+b2a+a2b)≥21(5+22×2)=29,当且仅当 a2b=b2a,即 a=b=32 时,等号成立.
因此,2a+bab 的最大值为 92,当且仅当 a=b=32 时取到.
已知 a,b>0,且 a1+b2=1,求 a−13+b−22 的最小值.
由 a1+b2=1 得 ab−2a−b=0,即 (a−1)(b−2)=2.因此
a−13+b−22=(a−1)(b−2)2a+3b−8=22a+3b−8=a+23b−4=(a+23b)(a1+b2)−4=4+2a3b+b2a−4≥23,当且仅当 2a3b=b2a,即有序数对 (a,b)=(3+1,36+23)或(−3+1,36−23) 时等号成立.
因此 a−13+b−22 的最小值为 23.
如果 连续使用 基本不等式,则取等条件为每次基本不等式的取等条件的交.
已知 a,b>0,求 a1+b2a+b 的最小值.
为了使所有项之积为常数,我们把 b 拆成 2b+2b.即
a1+b2a+b=a1+b2a+2b+2b≥44a1⋅b2a⋅2b⋅2b=4441=22,当且仅当 a1=b2a=2b,即 a=b=2 时等号成立.
因此,a1+b2a+b 的最小值为 22.
当然,也可以用两次基本不等式,先把前两项合并,再合并第三项,取等条件为两次基本不等式的取等条件 同时成立.
若 a,b∈R 且 ab>0,求 aba4+4b4+1 的最小值.
aba4+4b4+1≥ab24a4b4+1=ab4a2b2+1=4ab+ab1≥24ab⋅ab1=4.当且仅当 ⎩⎨⎧a4=4b4,4ab=ab1, 即 ⎩⎨⎧x=248,y=242 或 ⎩⎨⎧x=−248,y=−242 时等号成立.
因此,aba4+4b4+1 的最小值为 4.
所谓的配凑法,顾名思义,就是将所给的式子配凑出 和或积为定值 的形式,如 6x(3−2x)=3⋅2x(3−2x)、x+x−21=x−2+x−21+2,然后利用上面所说的方法求最值.
对于 二次比一次 的分式,一般 将分子表示成关于分母的二次多项式 的形式.如果直接配凑过于麻烦,也可以直接将分母 换元.
对于 一次比二次 的分式,一般先把分子 换元,然后把分子除到分母上,这样分母就变为 at+tb+c 的形式.注意在分母上应用基本不等式要变号.
若 x<1,求 x−1x2−x+9 的最大值.
x−1<0,因此
x−1x2−x+9=x−1(x−1)2+(x−1)+9=x−1+x−19+1≤−29+1=−5,当且仅当 x−1=x−19,即 x=−2 时等号成立.
因此 x−1x2−x+9 的最大值为 −5.
已知 x,y>0,x+3y+xy=9,求 x+3y 的最小值.
设法构造出 x+3y.由 x+3y+xy=9 得
x+3y=9−xy=9−31⋅x⋅3y≥9−31⋅4(x+3y)2,当且仅当 x=3y,即 x=3,y=1 时等号成立.设 x+3y=t>0,则上式即为
t≥9−121t2,解得 t≥6.
因此 x+3y 的最小值为 6,当且仅当 x=3,y=1 时取到最小值.
若对任意实数 x,y>0,不等式 x+xy≤a(x+y) 恒成立,求实数 a 的取值范围.
分离参数 得
a≥x+yx+xy.上式恒成立,即 a 大于等于 x+yx+xy 的 最大值.
注意到分子中有 x,x1/2,分母中有 x,x0,上下除以 x 得
x+yx+xy=1+xy1+xy.令 xy=t>0,则上式即 1+t1+t.
令 1+t=m>1,则 t=(m−1)2,于是上式即
1+(m−1)2m=m2−2m+2m=m+m2−21≤22−21=22+1,当且仅当 m=m2,即 m=2,即 t=xy=3−22 时等号成立.
所以 x+yx+xy 的最大值为 22+1,因此 a 的取值范围是 [22+1,+∞).
已知 x,y∈R,且 5x2y2+y4=1,求 x2+y2 的最小值.
注意到所给式子中三项的 y 的次数分别为 0,2,4,两侧除以 y2 得
5x2+y2=y21.根据 消元 的思想,将 x2 用含 y2 的式子表示,有
x2=51(y21−y2).于是
x2+y2=51(y21−y2)+y2=51(y21+4y2)≥51⋅24=54,当且仅当 y2=21,x2=103 时等号成立.
因此 x2+y2 的最小值为 54.


