跳到主要内容

有关三角函数的计算

同角三角函数的关系​

所谓同角三角函数，指的就是对同一个角 α\al 来说的 sin⁡α,cos⁡α,tan⁡α\sin\al,\cos\al,\tan\al 三个值．下面研究它们之间的关系．

根据定义，设旋转角 α\al 的终边与单位圆的交点为 P(x,y)P(x,y)，∣OP∣=r|OP|=r，则 sin⁡α=yr,cos⁡α=xr,tan⁡α=yx\sin\al=\df yr,\cos\al=\df xr,\tan\al=\df yx，且 x2+y2=r2x^2+y^2=r^2．故有：

三角恒等式
sin⁡2α+cos⁡2α=1. \sin^2\al+\cos^2\al=1.
推论
(sin⁡α+cos⁡α)2=1+2sin⁡αcos⁡α,(sin⁡α−cos⁡α)2=1−2sin⁡αcos⁡α,(sin⁡α+cos⁡α)2+(sin⁡α−cos⁡α)2=2,(sin⁡α−cos⁡α)2=(sin⁡α+cos⁡α)2−4sin⁡αcos⁡α.\bal &(\sin\al+\cos\al)^2=1+2\sin\al\cos\al, \\ &(\sin\al-\cos\al)^2=1-2\sin\al\cos\al, \\ &(\sin\al+\cos\al)^2+(\sin\al-\cos\al)^2=2, \\ &(\sin\al-\cos\al)^2=(\sin\al+\cos\al)^2-4\sin\al\cos\al. \eal

即 sin⁡α+cos⁡α\sin\al+\cos\al、sin⁡α−cos⁡α\sin\al-\cos\al、sin⁡αcos⁡α\sin\al\cos\al 三式，知一可推二．

切化弦公式
tan⁡α=sin⁡αcos⁡α,α≠kπ+π2,k∈Z.\tan\al=\df{\sin\al}{\cos\al},\quad\al\ne k\pi+\df\pi2,k\in\Z.

由此，可以将所有含 sin⁡α,cos⁡α,tan⁡α\sin\al,\cos\al,\tan\al 的式子化成只含有 sin⁡α\sin\al 和 cos⁡α\cos\al 的式子．

*拓展

引入余割函数 y=csc⁡x=1sin⁡xy=\csc x=\df1{\sin x}、正割函数 y=sec⁡x=1cos⁡xy=\sec x=\df1{\cos x}、余切函数 y=cot⁡x=1tan⁡xy=\cot x=\df1{\tan x}，有如下完整版公式：

  1. 平方关系： sin⁡2α+cos⁡2α=1,tan⁡2α+1=sec⁡2α,1+cot⁡2α=csc⁡2α. \sin^2\al+\cos^2\al=1,\quad\tan^2\al+1=\sec^2\al,\quad1+\cot^2\al=\csc^2\al.
  2. 乘积关系： sin⁡α=cos⁡α⋅tan⁡α,cos⁡α=sin⁡α⋅cot⁡α,tan⁡α=sin⁡α⋅sec⁡α,csc⁡α=sec⁡α⋅cot⁡α,sec⁡α=csc⁡α⋅tan⁡α,cot⁡α=csc⁡α⋅cos⁡α.\bga \sin\al=\cos\al\cdot\tan\al,\quad\cos\al=\sin\al\cdot\cot\al,\quad\tan\al=\sin\al\cdot\sec\al,\\ \csc\al=\sec\al\cdot\cot\al,\quad\sec\al=\csc\al\cdot\tan\al,\quad\cot\al=\csc\al\cdot\cos\al. \ega
  3. 倒数关系： tan⁡α⋅cot⁡α=1,sin⁡α⋅csc⁡α=1,cos⁡α⋅sec⁡α=1. \tan\al\cdot\cot\al=1,\quad\sin\al\cdot\csc\al=1,\quad\cos\al\cdot\sec\al=1.

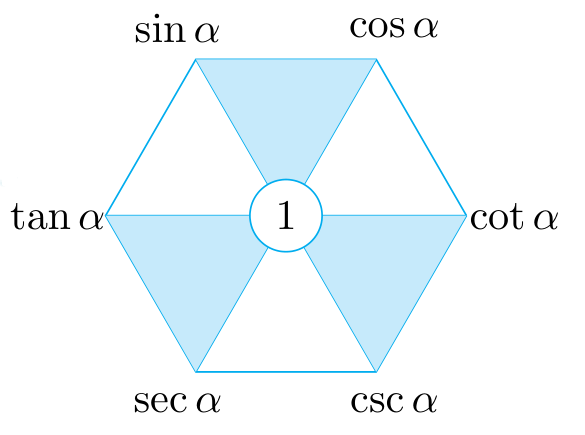
记忆方法：平方看三角，乘积看中间，倒数看对角线．

同角三角函数的关系

诱导公式​

所谓诱导公式，其实就是 sin⁡\sin、cos⁡\cos、tan⁡\tan 的自变量为 ±α+kπ2\pm\al+k\df\pi2 时，其值与 sin⁡α,cos⁡α,tan⁡α\sin\al,\cos\al,\tan\al 之间的各种等量关系．

诱导公式一（周期性）

sin⁡(α+2kπ)=sin⁡α\sin(\al+2k\pi)=\sin\al，cos⁡(α+2kπ)=cos⁡α\cos(\al+2k\pi)=\cos\al，tan⁡(α+kπ)=tan⁡α\tan(\al+k\pi)=\tan\al，其中 k∈Zk\in\Z．

诱导公式二（奇偶性）

sin⁡(−α)=−sin⁡α\sin(-\al)=-\sin\al，cos⁡(−α)=cos⁡α\cos(-\al)=\cos\al，tan⁡(−α)=−tan⁡α\tan(-\al)=-\tan\al．

诱导公式三

sin⁡(π+α)=−sin⁡α\sin(\pi+\al)=-\sin\al，cos⁡(π+α)=−cos⁡α\cos(\pi+\al)=-\cos\al，tan⁡(π+α)=tan⁡α\tan(\pi+\al)=\tan\al．

诱导公式四

sin⁡(π−α)=sin⁡α\sin(\pi-\al)=\sin\al，cos⁡(π−α)=−cos⁡α\cos(\pi-\al)=-\cos\al，tan⁡(π−α)=−tan⁡α\tan(\pi-\al)=-\tan\al．

诱导公式五

sin⁡(π2+α)=cos⁡α\sin\left(\df\pi2+\al\right)=\cos\al，cos⁡(π2+α)=−sin⁡α\cos\left(\df\pi2+\al\right)=-\sin\al，*tan⁡(π2+α)=cot⁡α\tan\left(\df\pi2+\al\right)=\cot\al．

诱导公式六

sin⁡(π2−α)=cos⁡α\sin\left(\df\pi2-\al\right)=\cos\al，cos⁡(π2−α)=sin⁡α\cos\left(\df\pi2-\al\right)=\sin\al，*tan⁡(π2−α)=cot⁡α\tan\left(\df\pi2-\al\right)=\cot\al．

口诀：奇变偶不变，符号看象限．

应用口诀的步骤：

  1. 首先假设 α\al 是 第一象限角（不管真正的 α\al 多大）．
  2. 「奇变偶不变」：如果 kk 为奇数，则 函数名 改变，否则不变，例如 sin⁡\sin 变成 cos⁡\cos，tan⁡\tan 变成 cot⁡\cot．
  3. 「符号看象限」：将 α\al 旋转 到自变量 kπ2±αk\df\pi2\pm\al 的位置，看 原函数名 在当前的象限是正值还是负值，添加正负号．

例如：

  • cos⁡(π−α)\cos\left(\pi-\al\right)：
    1. k=2k=2 为偶数，故结果为 cos⁡\cos；
    2. 将第一象限角 α\al 先对称到 −α-\al，再逆时针旋转 π rad\pi\,\mathrm{rad}，最终落在第二象限，由于 cos⁡\cos 在第二象限为负值，所以加负号；
    3. 因此，最终结果为 −cos⁡α-\cos\al．
  • sin⁡(3π2+α)\sin\left(\df{3\pi}2+\al\right)：
    1. k=3k=3 为奇数，故结果为 cos⁡\cos；
    2. 将第一象限角 α\al 逆时针旋转 3π2 rad\df{3\pi}2\,\mathrm{rad}，最终落在第四象限，由于 sin⁡\sin 在第四象限为负值，所以加负号；
    3. 因此，最终结果为 −cos⁡α-\cos\al．

三角恒等变换​

和差角公式​

两角和与差的正弦、余弦、正切公式
sin⁡(α±β)=sin⁡αcos⁡β±cos⁡αsin⁡β,cos⁡(α±β)=cos⁡αcos⁡β∓sin⁡αsin⁡β,tan⁡(α±β)=tan⁡α±tan⁡β1∓tan⁡αtan⁡βα,β,α±β≠kπ+π2,k∈Z.\bal &\sin(\al\pm\be)=\sin\al\cos\be\pm\cos\al\sin\be, \\ &\cos(\al\pm\be)=\cos\al\cos\be\mp\sin\al\sin\be, \\ &\tan(\al\pm\be)=\fr{\tan\al\pm\tan\be}{1\mp\tan\al\tan\be}\quad\al,\be,\al\pm\be\ne k\pi+\fr\pi2,k\in\Z. \eal

二倍角公式​

二倍角公式
sin⁡2α=2sin⁡αcos⁡α,cos⁡2α=cos⁡2α−sin⁡2α,tan⁡2α=2tan⁡α1−tan⁡2α.\bal &\sin 2\al=2\sin\al\cos\al, \\ &\cos 2\al=\cos^2\al-\sin^2\al, \\ &\tan 2\al=\fr{2\tan\al}{1-\tan^2\al}. \eal
推论 1（升幂公式）
cos⁡2α=cos⁡2α−sin⁡2α=2cos⁡2α−1=1−2sin⁡2α,sin⁡2α=2sin⁡αcos⁡α=(sin⁡α+cos⁡α)2−1=1−(sin⁡α−cos⁡α)2.\bga \cos 2\al=\cos^2\al-\sin^2\al=2\cos^2\al-1=1-2\sin^2\al,\\ \sin 2\al=2\sin\al\cos\al=(\sin\al+\cos\al)^2-1=1-(\sin\al-\cos\al)^2. \ega
推论 2（降幂公式）
cos⁡2α=1+cos⁡2α2,sin⁡2α=1−cos⁡2α2,sin⁡αcos⁡α=12sin⁡2α,tan⁡2α=1−cos⁡2α1+cos⁡2α.\bga &\cos^2\al=\fr{1+\cos 2\al}2, \\ &\sin^2\al=\fr{1-\cos 2\al}2, \\ &\sin\al\cos\al=\fr12\sin 2\al, \\ &\tan^2\al=\fr{1-\cos 2\al}{1+\cos 2\al}. \ega

用升幂公式和降幂公式可以将式子中的各个三角函数的次数统一．

推论 3
tan⁡α±tan⁡β=(tan⁡α±β)(1∓tan⁡αtan⁡β),tan⁡αtan⁡β=1−tan⁡α+tan⁡βtan⁡(α+β)=tan⁡α−tan⁡βtan⁡(α−β)−1.\bga \tan\al\pm\tan\be&=(\tan\al\pm\be)(1\mp\tan\al\tan\be),\\ \tan\al\tan\be&=1-\fr{\tan\al+\tan\be}{\tan(\al+\be)}=\fr{\tan\al-\tan\be}{\tan(\al-\be)}-1. \ega

即 tan⁡(α±β)\tan(\al\pm\be)、tan⁡αtan⁡β\tan\al\tan\be、tan⁡α±tan⁡β\tan\al\pm\tan\be 三式，知二可推一．

推论 4（万能公式）
sin⁡2α=2sin⁡αcos⁡αsin⁡2α+cos⁡2α=2tan⁡α1+tan⁡2α,cos⁡2α=cos⁡2α−sin⁡2αcos⁡2α+sin⁡2α=1−tan⁡2α1+tan⁡2α,\bal \sin2\al&=\fr{2\sin\al\cos\al}{\sin^2\al+\cos^2\al}=\fr{2\tan\al}{1+\tan^2\al},\\ \cos2\al&=\fr{\cos^2\al-\sin^2\al}{\cos^2\al+\sin^2\al}=\fr{1-\tan^2\al}{1+\tan^2\al},\\ \eal

用万能公式可以将所有 sin⁡x,cos⁡x,tan⁡x\sin x,\cos x,\tan x 都用 u=tan⁡x2u=\tan\df x2 换元，进而变为单变量的式子．

推论 5
sin⁡α1+cos⁡α=1−cos⁡αsin⁡α=tan⁡α2. \fr{\sin\al}{1+\cos\al}=\fr{1-\cos\al}{\sin\al}=\tan\fr\al2.

辅助角公式​

辅助角公式

设 a,b≠0a,b\ne0，则

asin⁡α+bcos⁡α=a2+b2sin⁡(α+φ),其中 tan⁡φ=ba. a\sin\al+b\cos\al=\sqrt{a^2+b^2}\sin(\al+\ph),\quad\text{其中}\,\tan\ph=\fr ba.

例如：

  • sin⁡x+cos⁡x=2sin⁡(x+π4)\sin x+\cos x=\sqrt2\sin\left(x+\df\pi4\right)；
  • sin⁡x+3cos⁡x=2sin⁡(x+π3)\sin x+\sqrt3\cos x=2\sin\left(x+\df\pi3\right)；
  • 3sin⁡x+cos⁡x=2sin⁡(x+π6)\sqrt3\sin x+\cos x=2\sin\left(x+\df\pi6\right)．