简谐运动

弹簧振子中的运动学变量

水平弹簧振子

观察下面这个模型：

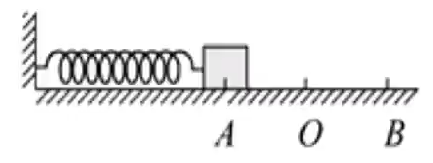
设弹簧处于原长时，端点处于 $O$ 点．用外力将物体移动到 $A$ 点后撤去外力，设地面绝对光滑，则物体会在 $AB$ 两点间永不停歇地往返移动．

这个运动模型称作 弹簧振子，弹簧上挂载的物体称作 振子；物体所受合外力为 $0$ 的位置称作 平衡位置；物体所受弹力为 $0$ 的点为 弹簧原长点．在水平弹簧振子模型中，物体所受的合外力就是弹力，因此平衡位置与弹簧原长点为同一位置 $O$．

一个约定俗成：以 平衡位置 为原点，向右为 $x$ 轴正方向建立一维坐标系，则物体处于 $P$ 点时，称 $\overrightarrow{OP}$ 为物体此时的 位移，是一个矢量．

位移、速度 与 加速度 均采用矢量的「有符号表达」，即用一个有符号标量同时代表对应矢量的方向和大小．

值得指出的是，比较位移、速度、加速度大小时比的是绝对值．如 $\pu{-3m}$ 应视作比 $\pu{-5m}$ 小，比 $\pu{2m}$ 大．

信息

接下来请读者尝试填下面这个表（非常建议读者尝试自己填写一下这 24 个空，然后再和下面的答案对，不要直接看答案）：

	$\boldsymbol x$ 变大 / 变小？	$\boldsymbol a$ 变大 / 变小？	$\boldsymbol v$ 变大 / 变小？	$\boldsymbol x$ 正负？	$\boldsymbol a$ 正负？	$\boldsymbol v$ 正负？
$A \to O$
$O \to B$
$B \to O$
$O \to A$

答案

	$\boldsymbol x$ 变大 / 变小？	$\boldsymbol a$ 变大 / 变小？	$\boldsymbol v$ 变大 / 变小？	$\boldsymbol x$ 正负？	$\boldsymbol a$ 正负？	$\boldsymbol v$ 正负？
$A \to O$	$\darr$	$\darr$	$\uarr$	$-$	$+$	$+$
$O \to B$	$\uarr$	$\uarr$	$\darr$	$+$	$-$	$-$
$B \to O$	$\darr$	$\darr$	$\uarr$	$+$	$-$	$-$
$O \to A$	$\uarr$	$\uarr$	$\darr$	$-$	$+$	$+$

为了更直观的理解，这里给出六个物理量的实际意义：

• $x$ 的大小：小球与平衡位置的距离．变大等价于小球远离平衡位置，变小等价于小球接近平衡位置．
• $v$ 的大小：字面意思．
• $a$ 的大小：字面意思．小球加速度与小球所受外力大小成正比．
• $x$ 的正负：小球相对于平衡位置的方向．为正说明小球在平衡位置的右侧，为负说明小球在平衡位置的左侧．
• $v$ 的正负：小球移动的方向．为正说明小球向右移动，为负说明小球向左移动．
• $a$ 的正负：字面意思．与小球所受合外力的方向相同．

我们有如下性质：

• $a$ 的正负不决定 $v$ 的变大变小，$v$ 的正负并不决定 $x$ 的变大与变小．这是因为比较位移、速度、加速度大小时，比的是绝对值（如果比较的是原值的话，这些性质理应成立）．
• $x$、$a$ 成正相关，总具有 相同 的 变化趋势．
• $v$ 与上面两个变量总具有 相反 的 变化趋势．
• $x$ 与 $a$ 总是拥有 相反 的 符号．

后三条性质可以总结三句话：

• 物体所受 $F_合$ 始终指向平衡位置（体现为 $x$ 与 $a$ 始终异号）．
• 物体 远离 平衡位置（$x$ 变大）时，加速度必 变大（$a$ 变大）、物体必 减速（$v$ 变小）．
• 物体 接近 平衡位置（$x$ 变小）时，加速度必 变小（$a$ 变小）、物体必 加速（$v$ 变大）．

非水平弹簧振子

考虑将上面的水平面做一定倾斜，或者直接将整个系统竖立（此时可撤去小球的支撑面），如：

将物体从平衡位置向下压至点 $B$ 后释放，不计任何阻力，则小球将永不停息地在 $AB$ 间往复移动．

我们仍然将物体所受合外力为 $0$ 的位置 $O$ 称作 平衡位置，物体所受弹力为 $0$ 的点 $O'$ 称作 弹簧原长点．与水平弹簧振子不同的是，此时物体所受的合外力包括弹力与重力两个力，于是 $O$ 与 $O'$ 不再重合，$O'$ 应该在 $O$ 的上方，因为点 $O$ 处弹簧仍然存在向上的弹力．

如果我们以 平衡位置 $O$ 为原点（注意不是 $O'$）建立一维坐标系，定义向上为正方向，向下为负方向，同理可以定义出振子的 位移．

两个弹簧振子的共同点

这三条性质在两个弹簧振子中均成立：

• 物体所受 $F_合$ 始终指向平衡位置（体现为 $x$ 与 $a$ 始终异号）．
• 物体 远离 平衡位置（$x$ 变大）时，受力必 变大（$F_合$ 变大）、加速度必 变大（$a$ 变大）、物体必 减速（$v$ 变小）．
• 物体 接近 平衡位置（$x$ 变小）时，受力必 变小（$F_合$ 变小）、加速度必 变小（$a$ 变小）、物体必 加速（$v$ 变大）．

也即：

• 关于方向，$a$ 与 $x$ 一定异号（方向相反）．$v$ 与它们的正负没有必然联系．
• 关于变化趋势，$a$，$x$ 一定是一个趋势，$v$ 一定是另一个趋势．

记住这个结论有助于做选择时更快得到答案，它们的背后原因已经在上面解释．

$a$，$v$ 的最值点：

• $A$、$B$ 处：速度 $v$ 取到最小值 $0$；加速度 $a$ 取到最大值.
• $O$ 处：速度 $v$ 取到最大值；加速度 $a$ 取到最小值 $0$．

再考虑 $F_合$，$E_{\mathrm k}$，$E_{\mathrm p总}$，$E_{\mathrm p弹}$：

• $F_合$ 的变化趋势、最值点与 $a$ 一致．
• $E_{\mathrm k}$ 的变化趋势、最值点与 $v$ 一致．
• $E_{\mathrm p总}$ 的变化趋势、最值点与 $v$ 相反（最值点相反的含义是：$v$ 的最大值点为 $E_{\mathrm p总}$ 的最小值点，$v$ 的最小值点同理）．
• 水平弹簧振子中，$E_{\mathrm p弹} = E_{\mathrm p总}$．
• 竖直弹簧振子中，$E_{\mathrm p弹}$ 与其它物理量无必然联系．
• $E_{\mathrm p弹}$ 取到最小值 $0$ 的点为 $O'$．
• $E_{\mathrm p弹}$ 取到最大值的点在 $B$．注意，竖直弹簧振子中，点 $A$ 处弹性势能取不到最大值（想一想为什么？）．

例题 1.1

（多选）如图所示，一小球在弹簧上方 $B$ 点由静止释放，初始时 $B$ 点位置弹簧处于原长状态，小球下落的最低点记为 $A$ 点，此后小球在 $AB$ 之间做往复运动．关于小球的运动分析，下列说法错误的是：

• A. 弹簧处于原长时，小球的速度最大
• B. 小球从 $B$ 到 $A$ 的运动过程中，弹簧做功为 $0$
• C. 小球的速度增大时，加速度一定减小
• D. 小球向平衡位置移动时，弹性势能一定减小

例题 1.1 解答

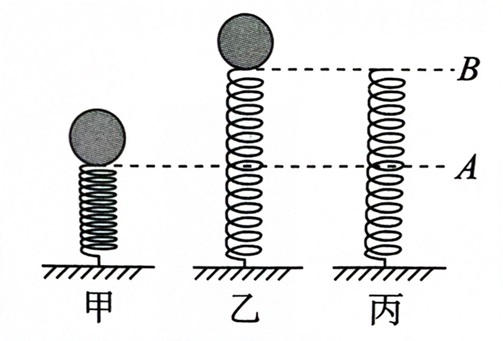
此题中，$B = O'$，而 $O$ 点没有画出，它应当在 $AB$ 的中点（至于为什么恰好是中点，学到后面会有答案）．

在竖直弹簧振子中，对 $\boldsymbol O$ 与 $\boldsymbol{O'}$ 的区分是必要的．

A. $O' = B$ 是速度最小值为 $0$ 的点，速度最大值点应为 $O$．A 错误．

B. 点 $A$ 与点 $B$ 的弹性势能不等．两个角度：

• $A$ 到 $B$ 弹簧从压缩状态到原长，弹性势能减小为 $0$，弹性势能一定做正功．
• $A$ 到 $B$ 是一个弹性势能转化为重力势能的过程（端点动能均为 $0$，不变）．

因此弹簧做功不可能为 $0$，B 错误．

C. $v$ 与 $a$ 变化趋势一定相反．C 正确．

D. 竖直弹簧振子中，$x$ 与 $E_{\mathrm p}$ 无必然联系．事实上，从 $O'$ 向 $O$ 的过程中，小球向平衡位置移动，弹性势能增大．D 错误．

故选 ABD．

如果将题目改为水平弹簧振子，则四个选项均正确．

例题 1.2

如图所示，在光滑地面上，一弹簧左端固定在墙壁上，右端连接一个物体，点 $O$ 为弹簧为原长时物体的位置．现对物体施加一外力，压缩弹簧，使物体在 $A$ 点保持平衡，现撤去外力，物体在 $AB$ 之间做往复运动．关于物体运动的分析，下列说法正确的是：

• A. 物体的位移方向总指向平衡位置
• B. 加速度方向总与位移方向相反
• C. 位移方向总与速度方向相反
• D. 速度方向总与位移方向相同

例题 1.2 解答

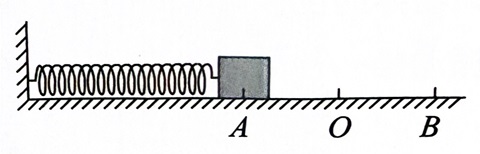
A. 物体的位移方向应该总是背离平衡位置．A 错误．

B. $a$ 与 $x$ 符号相反．B 正确．

C、D. $v$ 的符号与其它物理量不构成必然联系．C、D 均错误．

故选 B．