导数基本概念

*极限与连续

高中阶段不要求对极限的掌握，本章仅做了解即可，不做应试要求．

数列的极限

直观上看，数列 $a_n = \df 1 n$ 在 $n \to +\infty$ 时无限接近于 $0$．这个「无限接近于 $0$」到底如何严谨地刻画呢？

答案是魏尔斯特拉斯提出的，具有划时代意义的 $\varepsilon \text - N$ 语言：

对于数列 $\{a_n\}$，如果存在实数 $a$，使得 $\forall \varepsilon > 0$，$\exist N \in \N^\ast$，$\forall n > N$，有 $|a_n - a| < \varepsilon$，则称数列 $\{a_n\}$ 收敛于 $a$，$a$ 是 $\{a_n\}$ 的 极限，记作

$$\lim_{n \to \infty} a_n = a$$

也就是说，如果对于任意一个 $\varepsilon > 0$，我们都能找到这个数列的某一项，使得 从这一项起后面的任一项 与 $a$ 的距离均小于 $\varepsilon$，就称这个数列收敛于 $a$．

当一个数列不收敛时，称它是 发散 的．

例

用极限的定义证明 $a_n = \df 1 n$ 时，$\{a_n\}$ 收敛到 $0$．

解答

$$\lv \df 1 n - 0 \rv = \df 1 n < \varepsilon \iff n > \df 1 \varepsilon$$

因此，对任意 $\varepsilon > 0$，取 $N = \max\left\{\left\lfloor \df 1 \varepsilon \right\rfloor, 1\right\}$，则 $n > N$ 时，有

$$\lv \df 1 n - 0 \rv < \varepsilon$$

因此 $\lim\limits_{n \to +\infty} \df 1 n = 0$．

高中阶段不要求证明极限．数列 $\left\{\df 1 n\right\}$ 在 $n \to \infty$ 时趋于 $0$ 是一个可以直接写出的结论．

函数的极限

对于实数 $a$，称区间 $(a-\de,a+\de)$ 为 $a$ 的「$\de$ 邻域」，记为 $U_\de(a)$，其中 $\de$ 是一正实数（一般较小）．若 $\de$ 的大小是无关紧要的，则 $a$ 的邻域简记为 $U(a)$．

区间 $(a-\de,a)\cup(a,a+\de)$ 称为 $a$ 的「去心 $\de$ 邻域」，记为 $\mathring U_\de(a)$．

对于函数 $f(x)$ 及其定义域上实数 $x_0$，如果存在实数 $A$，使得 $\forall \varepsilon > 0$，$\exist \delta > 0$，对任意 $x \in \mathring U_\delta(x_0) = (x_0 - \delta, x_0) \cup (x_0, x_0 + \delta)$，有 $|f(x) - A| < \varepsilon$，则 $A$ 称作 $f(x)$ 在点 $x_0$ 处的 极限，记作

$$\lim_{x \to x_0} f(x) = A$$

这就是严格定义函数极限的 $\varepsilon \text - \delta$ 语言．也就是说，对于任意 $\varepsilon > 0$，我们都能找到一段定义域上 包含 $x_0$ 但是扣去 $x_0$ 的区间，使得这个区间上对应的函数值与 $A$ 的距离都小于 $\varepsilon$，就称函数在点 $x_0$ 处的极限为 $A$．

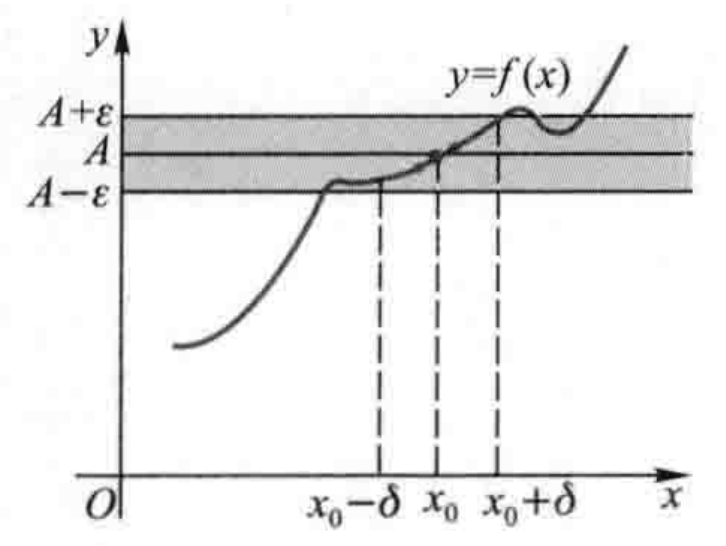
可以证明，函数在某点存在极限，则这个极限唯一．

函数极限的运算法则

假设极限 $\lim\limits_{x\to a}f(x)$ 和 $\lim\limits_{x\to a}g(x)$ 存在．

• $\lim\limits_{x \to a} [f(x) \pm g(x)] = \lim\limits_{x \to a} f(x) \pm \lim\limits_{x \to a} g(x)$．
• $\lim\limits_{x \to a} [f(x)g(x)] = \lim\limits_{x \to a} f(x) \cdot \lim\limits_{x \to a} g(x)$．
• 当 $\* \lim\limits_{x \to a} g(x) \ne 0$ 时，$\lim\limits_{x \to a} \df{f(x)}{g(x)} = \df{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)}$．
• 设 $y=f(\ph(x))$ 是由 $y=f(u)$ 和 $u=\ph(x)$ 复合而成的函数，其中 $\lim\limits_{x\to x_0}\ph(x)=u_0$ 且 $\ph(x)\ne u_0$，且 $\lim\limits_{u\to u_0}f(u)=A$，则 $$\lim\limits_{x\to x_0}f(\ph(x))=\lim\limits_{u\to u_0}f(u)=A.$$ 特别地，若 $f(u)$ 在 $u_0$ 附近连续，即 $\lim\limits_{u\to u_0}f(u)=f(u_0)=A$，则 $$\lim\limits_{x\to x_0}f(\ph(x))=f\left(\lim\limits_{x\to x_0}\ph(x)\right)=f(u_0)=A.$$

这些性质不难感性理解，也可以严格证明，证明高中阶段不作要求，这里不给出．

无穷小

若 $\lim\limits_{x \to a} f(x) = 0$，称 $f(x)$ 为 $x \to a$ 时的 无穷小．

根据上面的四则运算规则，可以得知：

• 若 $f(x)$，$g(x)$ 都是 $x \to a$ 时的无穷小，则 $f(x) \pm g(x)$ 是 $x \to a$ 时的无穷小．
• 若 $f(x)$ 是 $x \to a$ 时的无穷小，且 $\lim\limits_{x \to a} g(x)$ 存在（更宽松的条件是 $g(x)$ 在 $a$ 附近有上下界），则 $f(x) \cdot g(x)$ 是 $x \to a$ 时的无穷小．

但两个无穷小的商不能确定：运算法则规定了分母不能为无穷小．

设 $f(x)$，$g(x)$ 为 $x \to a$ 时的两个无穷小，且 $g(x) \ne 0$，当 $\lim\limits_{x \to a} \df{f(x)}{g(x)}$ 存在时，

• 若 $\lim\limits_{x \to a} \df{f(x)}{g(x)} = 0$，则称当 $x \to a$ 时，$f(x)$ 是 $g(x)$ 的 高阶无穷小．
• 若 $\lim\limits_{x \to a} \df{f(x)}{g(x)} = b \ne 0$，则称当 $x \to a$ 时，$f(x)$ 与 $g(x)$ 是 同阶无穷小．
• 特别地，若 $b = 1$ ，则称当 $x \to a$ 时，$f(x)$ 与 $g(x)$ 是 等价无穷小，记作 $f(x) \sim g(x)\quad(x \to a)$．

等价无穷小替换公式：设 $f(x) \sim F(x) \quad (x \to a)$，$g(x) \sim G(x) \quad (x \to a)$，则

$$\bal & \phantom = \lim\limits_{x \to a} \df{f(x)}{g(x)} \\ & = \lim\limits_{x \to a} \left[\df{F(x)}{G(x)} \cdot \df{f(x)}{F(x)} \cdot \df{G(x)}{g(x)}\right]\\ & = \lim\limits_{x \to a} \df{F(x)}{G(x)} \cdot \lim\limits_{x \to a} \df{f(x)}{F(x)} \cdot \lim\limits_{x \to a} \df{G(x)}{g(x)} \\ & = \lim\limits_{x \to a} \df{F(x)}{G(x)} \eal$$

也即对一个分式求极限时，分子与分母可以 替换为它的等价无穷小，而 极限值不改变，这个规则称作 等价无穷小替换规则．

一个最经典的等价无穷小是 $x \sim \sin x \sim \tan x \quad (x \to 0)$（证明从略）．

高中物理中一些公式的推导用到的，所谓「$x$ 很小，将 $\sin x$ 近似为 $x$」的原理，其实就是在做上面的 等价无穷小替换．

连续的定义

设函数 $f(x)$ 在点 $a$ 存在极限，且

$$\lim_{x \to a}f(x) = f(a)$$

称 $f(x)$ 在点 $a$ 连续．

可以证明，所有初等函数在定义域上都处处连续．

导数的定义

对连续函数 $f(x)$，令自变量从 $x$ 从 $x_0$ 出发，当自变量变化了 $\Delta x$ 时，因变量 $f(x)$ 会变化

$$\Delta f = f(x_0 + \Delta x) - f(x_0)$$

这个过程中，称因变量变化与自变量变化之比为 因变量的平均变化速度，即

$$\df{\Delta f}{\Delta x} = \df{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$$

这里的平均变化速度有两个意义需要体会：

• 物理意义：将 $f(x)$ 图像视作某个物体做直线运动的 $x \text - t$ 图像，则上式相当于从 $x_0$ 时刻开始的 $\Delta x$ 时间内，物体平均速度 的大小．
• 斜率意义：上式为点 $(x_0, f(x_0))$ 与 $(x_0 + \Delta x, f(x_0 + \Delta x))$ 的 连线斜率．

在物理中，物体的瞬时速度定义为上述平均速度中，将 $\Delta x$ 趋近于 $0$ 的结果．在数学上用极限表达就是

$$\lim_{\Delta x \to 0} \df{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$$

这是两个无穷小相比，当极限存在时，称 $f$ 在 $x_0$ 处 可导，此极限值为 $f$ 在 $x_0$ 处的 导数，记作

$$f'(x_0) = \lim_{\Delta x \to 0} \df{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$$

可以证明，函数在某点 可导 比函数在某点 连续 要 强．

其物理意义为瞬时速度，斜率意义为 切线斜率：

Loading

将 $B$ 拖至与 $A$ 无限接近，此时斜线的斜率会趋近一个值，这个值就是 $f$ 在 $x_A$ 处的 导数．

我们定义：一元函数在点 $x_0$ 处的 切线 为 过点 $(x_0, f(x_0))$ 且斜率为 $f'(x_0)$ 的直线，即

$$y - f(x_0) = f'(x_0)(x - x_0)$$

根据上面的讨论，对于一条过函数图线上某两点的 割线，让其中一点 沿着函数图线 无限 逼近 另一点，得到的直线即 切线．

:::warning（感觉表述不好 -ljh）

函数切线的定义与圆锥曲线中的切线定义有所不同．圆锥曲线中的切线的定义是一条 与圆锥曲线有且仅有一个交点 的直线，但一元函数的切线与函数本身的交点不一定只有一个．

不过，圆锥曲线的切线也可视作割线逼近的产物，一元函数的切线与圆锥曲线的切线都称作切线，正是这个原因．

:::

一般地，如果函数 $f(x)$ 在定义域 $D$ 内每一点都 可导，则称 $f(x)$ 可导．$\forall x \in D$，$f'(x)$ 唯一确定，因此 $f'(x)$ 是在 $D$ 上的一个函数，这个函数称作 导函数，简称 导数．求导 通常指的是求函数 $f$ 的 导函数 的过程．

初等函数不一定处处可导，如：

• $f(x) = |x| = \sqrt{x^2}$ 的图像为一个 V 形，在 $x = 0$ 处从两侧进行「割线逼近切线」，逼近出的切线斜率不同，左侧为 $-1$，右侧为 $1$，因此该函数在 $x = 0$ 不可导．
• $f(x) = \sqrt[3] x$ 在 $x = 0$ 的切线为竖直线，斜率不存在，因此该函数在 $x = 0$ 不可导．

对于这样的函数，其导函数在原函数的定义域上舍去不可导的部分（这两例中为 $0$），但这样的初等函数是少数．

因此，导函数 的 定义域 一定是 原函数 的 子集，并且在绝大多数情况下 两个定义域相同．

求导法则

基本初等函数的导数

由导数的定义和极限的性质可以推出（假设下面的函数都有定义）：

• 常函数 的导数：$C'=0$，其中 $C$ 为任意常数．
• 幂函数 的导数：$(x^\alpha)' = \red{\alpha}x ^{\red{\alpha - 1}}$，其中 $\al$ 为非零有理数．
• 三角函数 的导数：$(\sin x)' = \cos x$，$(\cos x)' = \red - \sin x$，*$(\tan x)'=\df1{\cos^2x}=\sec^2x$．
• 指数函数 的导数：$(a^x)' = a^x \ln a$，$(\log_a x)' = \df{1}{x \ln a}, \quad \red{x > 0}$．
• 指数函数 中 $a = \mathrm e$ 的情形值得注意：$(\e^x)' = \e^x$，$(\ln x)' = \df 1 x, \quad \red {x > 0}$．

其中 $\e$ 为自然对数 $\ln$ 的底，称为 自然常数，其值为 $2.718281828459\dots$．它是一个无理数．

必须指出，$\log_a x$ 的定义域为 $(0, +\infty)$，但其导数形式 $\df{1}{x \ln a}$ 的自然定义域是 $\{x \mid x \ne 0\}$，因此必须加上定义域 $(0, +\infty)$ 的限制．

*自然常数 $\e$ 可以定义为

$$\e = \lim_{x \to +\infty}\left(1 + \df 1 x\right)^x.$$

自然常数 $\e$ 与自然对数 $\ln$ 的特别意义到现在终于明显：它们在指对函数的求导上具有高度的基础性和特殊性．

导数的四则运算

由导数的定义和极限的性质可以推出：

$$\begin{array}{rcl} [f(x) \pm g(x)]' & = & f'(x) \pm g'(x),\\[1em] [f(x) \cdot g(x)]' & = & f'(x) \cdot g(x) + f(x) \cdot g'(x),\\[1em] \left[\dfrac{f(x)}{g(x)}\right]' & = & \dfrac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{g^2(x)}. \end{array}$$

除法求导法则的要点：上面先导，下面后导，中间是 减号．

推论：

$$[cf(x)]' = [c(x) \cdot f(x)]' = \red{c'(x) \cdot f(x)} + c(x) \cdot f'(x) = c(x) \cdot f'(x)$$

这里 $c$ 是常数，$c(x)$ 是常函数 $c(x) = c$．而 $c'(x) = 0$，因此标红的一项为 $0$．

这条规则的意义是：$f(x)$ 与 常数 相乘的导数，等于 $f(x)$ 的导数与常数相乘．

这里的常数不仅可以是数字，还可以是 与 $x$ 无关的参数，如 $f(x) = (a + 3)x^2$，则 $f'(x) = (a+3)\cdot(x^2)' = 2(a + 3)x$．

以及 $f(x) = \df{x^2}2$，$f(x) = \df{x^2}{a + 3}$，可以分别将常数视作 $\df 1 2$ 与 $\df 1 {a + 3}$ 来运用此规则（而不是运用除法导数运算法则）．

$$[\e^xf(x)]' = (\e^x)' \cdot f(x) + \e^x \cdot [f(x)]' = \e^x \cdot [f(x) + f'(x)]$$

复合函数的导数

复合函数的求导法则：设

• 函数 $u=g(x)$ 在点 $x$ 处可导，即 $u'_x=g'(x)$；
• 函数 $y=f(u)$ 在点 $u=g(x)$ 处可导，即 $y'_u=f'(u)=f'(g(x))$，

则复合函数 $y=f(g(x))$ 在该点 $x$ 处可导，且

$$[f(g(x))]'=f'(g(x))g'(x).$$

注意区分 $[f(\ph(x))]'$ 和 $f'(\ph(x))$：

• 前者指的是函数 $g(x)=f(\ph(x))$ 对自变量 $x$ 的导数在点 $x$ 处的取值；
• 后者指的是函数 $f(u)$ 对自变量 $u$ 的导数在点 $u=\ph(x)$ 处的取值．

例 1

求 $y=\sin 2x$ 的导数．

例 1 解答

令 $y=\sin u$，$u=2x$，则 $y'(x)=y'(u)\cdot u'(x)=\cos u\cdot 2=2\cos 2x$．

熟练之后，可以不用设中间变量：$(\sin2x)'=\cos2x\cdot(2x)'=2\cos2x$．

例 2

求 $y=\sqrt{1+x^2}$ 的导数．

例 2 解答

令 $y=\sqrt u=u^{1/2}$，$u=1+x^2$，则 $y'(u)=\dfrac12u^{-1/2}=\dfrac1{2\sqrt u}$，$u'(x)=2x$，故

$$y'(x)=y'(u)\cdot u'(x)=\frac1{2\sqrt u}\cdot(2x)=\frac{x}{\sqrt{1+x^2}}.$$

即 $\left(\sqrt{1+x^2}\right)'=\dfrac{(1+x^2)'}{2\sqrt{1+x^2}}=\dfrac{x}{\sqrt{1+x^2}}$．

由归纳原理，可以推出多次复合的函数的导数公式：

$$[f(g(h(x)))]'=f'(g(h(x)))\cdot g'(h(x))\cdot h'(x).$$

例 3

求 $y=f(x)=\ln\cos\sqrt x$ 的导数．

例 3 解答

设 $y(u)=\ln u$，$u(v)=\cos v$，$v(x)=\sqrt x$，则

$$y'(u)=\frac1u,\quad u'(v)=-\sin v,\quad v'(x)=\frac{1}{2\sqrt x},$$

故

$$y'(x)=y'(u)\cdot u'(v)\cdot v'(x)=\frac1{\cos\sqrt x}\cdot(-\sin\sqrt x)\cdot\frac1{2\sqrt x}=-\frac{\tan\sqrt x}{2\sqrt x}.$$

*Leibniz 记号：$y=f(x)$ 的导函数 $y'=f'(x)$ 记为 $\dfrac{\mathrm{d}y}{\mathrm{d}x}$，$x_0$ 处的导数 $f'(x_0)$ 记为 $\dfrac{\mathrm{d}y}{\mathrm{d}x}\bigg\vert_{x=x_0}$．

用 Leibniz 记号可以方便地表示复合函数的求导法则：设 $y=y(u)$，$u=u(x)$，则

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}u}\frac{\mathrm{d}u}{\mathrm{d}x}.$$

设 $y=y(u)$，$u=u(v)$，$v=v(x)$，则

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}u}\frac{\mathrm{d}u}{\mathrm{d}v}\frac{\mathrm{d}v}{\mathrm{d}x}.$$