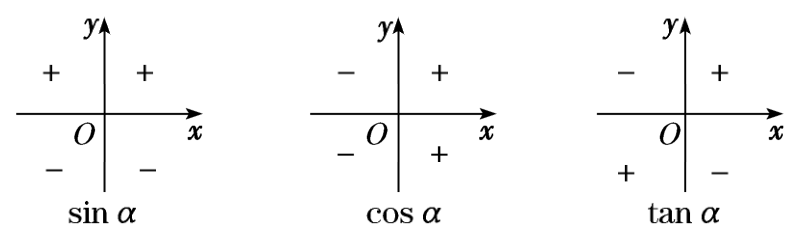初中所学的角仅限于 0∘ 到 180∘ 之间的角,而研究的三角函数也仅限于锐角三角函数.在这一节中,我们将要把角度的范围与三角函数的定义域推广到实数域 R.
一条射线绕其端点旋转,开始时的位置与旋转后的位置之间形成的夹角叫做 旋转角,起始位置与最终位置分别叫做 始边 和 终边.
我们规定,按 逆时针 方向旋转形成的旋转角为 正角,按 顺时针 方向则为 负角.如果没有任何旋转,则为 零角.任意角包括正角、负角、零角.如图所示.
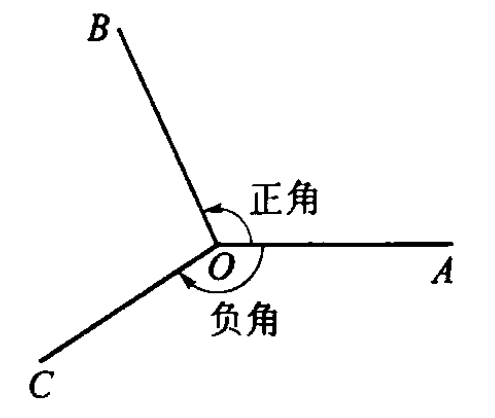
类似数轴上的数,规定 角的加法:在角 α 的基础上按逆时针将终边旋转角 β,得到的总旋转角规定为 α+β.同时,规定按不同方向旋转相同的量所成的两个角叫做互为 相反角,角 α 的相反角记作 −α.这样可以规定 角的减法:α+(−β)=α−β.
下面默认在平面直角坐标系 xOy 中讨论角,使角的顶点与原点重合,角的始边与 x 轴的非负半轴重合.
终边在第几象限,就说这个角是第几 象限角.如果角的终边在坐标轴上,认为这个角不属于任何一个象限,常称为 轴线角.
所有与角 α 终边相同的角(包括角 α 自身)构成的集合为 S={β∣β=α+k×360∘,k∈Z}.
我们知道,角可以用度(∘)为单位进行度量,1∘ 等于周角的 3601.这种单位制称为 角度制.在角度制中,除了度,还有更小的单位分(′)、秒(′′).他们之间的换算关系是:
1∘=60′,1′=60′′.
为了数学和其他科学研究的方便,引入了 弧度制.
我们规定:长度等于半径长的圆弧所对的圆心角叫做 1 弧度 的角,弧度单位用 rad 表示.如图所示.
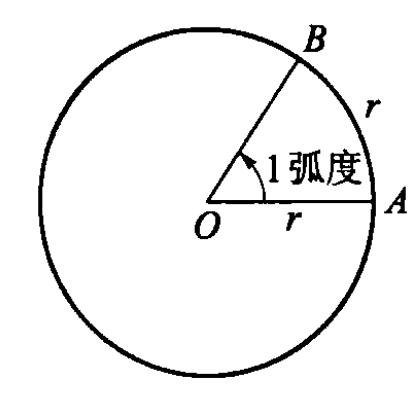
一般地,在半径为 r 的圆中,设弧长为 l 的弧所对的圆心角为 αrad,则
∣α∣=rl.
由此有扇形面积公式
S=21lr=21∣α∣r2.
根据 180∘=πrad 可以进行角度与弧度的换算,设 a∘=α,则
a∘α=α×π180∘,=a∘×180∘π.
弧度是一个无量纲单位,定义为 1 rad=1.因此,弧度单位 rad 常常省略不写.当在没有任何符号的情况下量化角度时,假设为弧度;当表示度数时,使用度符号 ∘.
欧拉用弧度制将圆弧与线段的度量相统一.弧度制具有十分优美的性质,例如:
- 欧拉公式 eix=cosx+isinx;
- 泰勒级数展开 sinx=x−3!x3+5!x5−7!x7+⋯;
- 重要极限 x→0limxsinx=1;
- 角速度公式 ω=rv.
常用角度与弧度的对应关系如下表:
| 角度 | 0∘ | 15∘ | 30∘ | 45∘ | 60∘ | 75∘ |
|---|
| 弧度 | 0 | 12π | 6π | 4π | 3π | 125π |
| 角度 | 90∘ | 120∘ | 135∘ | 150∘ | 180∘ | 360∘ |
| 弧度 | 2π | 32π | 43π | 65π | π | 2π |
在平面直角坐标系 xOy 中,称圆心为原点、半径为 1 的圆为 单位圆.设角 α(α∈R)的终边与单位圆的交点为 P(x,y).
一般地,
- 规定 α 的 正弦函数 为纵坐标 y,即 y=sinα;
- 规定 α 的 余弦函数 为横坐标 x,即 x=cosα;
- 规定 α 的 正切函数 为纵坐标与横坐标的比值,即 xy=tanα(x=0).
如下图所示.
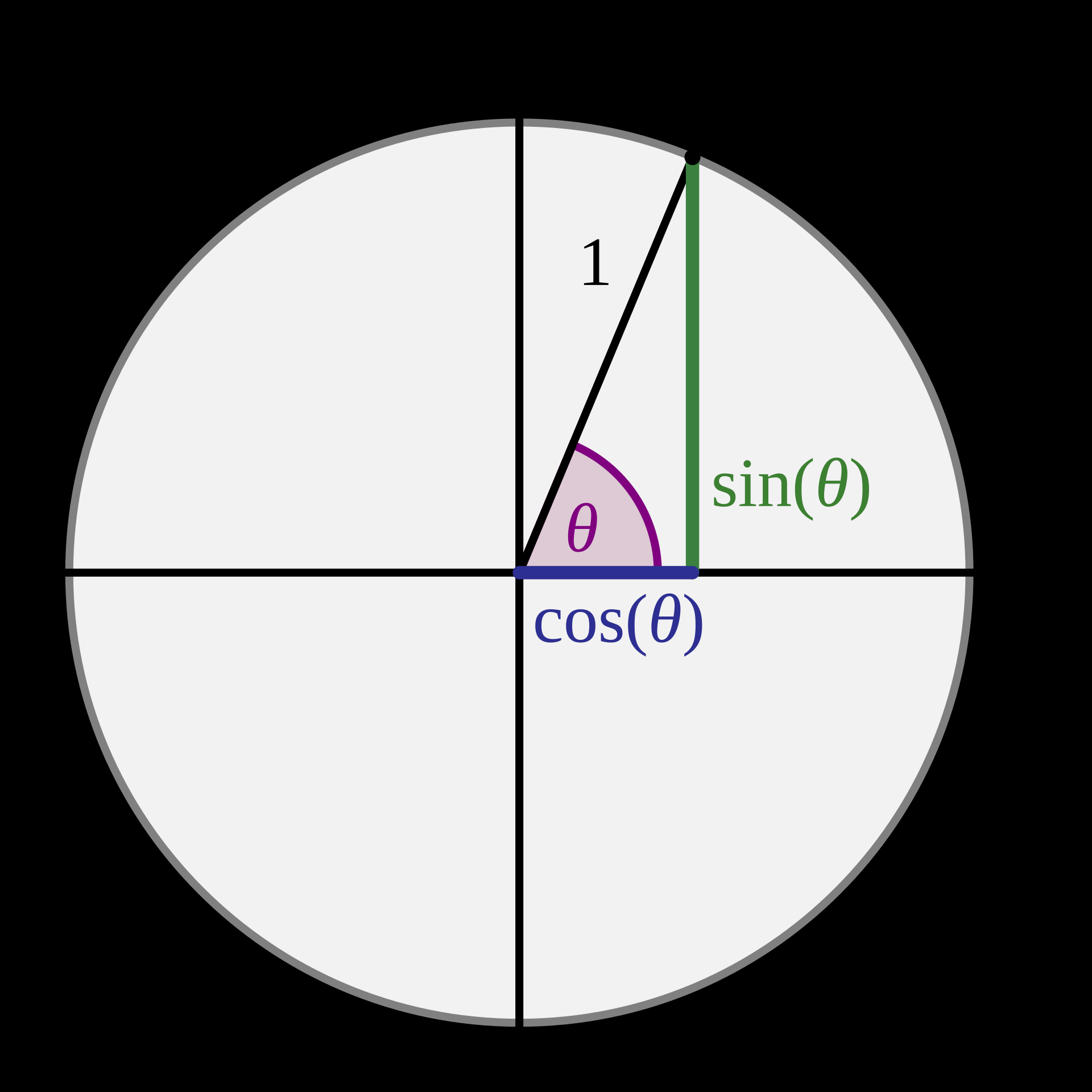
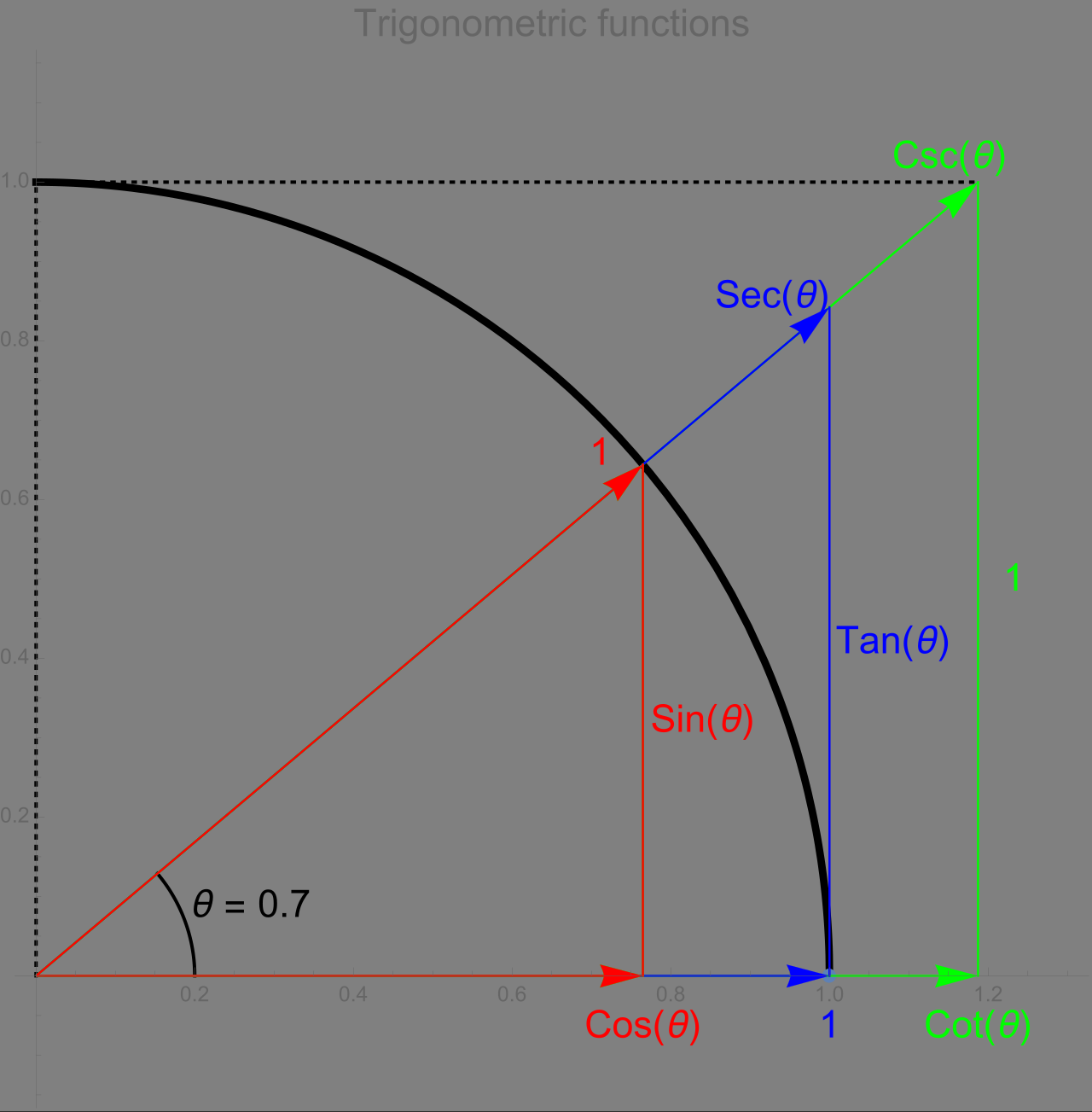
当终边在 y 轴上时,x=0,xy 无意义,故 tanα 的定义域为 {α∣α=2π+kπ,k∈Z}.
一般地,设角 α 的终边与圆心为原点、半径为 r 的圆的交点为 P(x,y),则
sinα=ry=x2+y2y,cosα=rx=x2+y2x,tanα=xy.
由于 r=x2+y2>0,可以确定各个象限角与轴线角的三角函数的正负情况,如下图和下表:
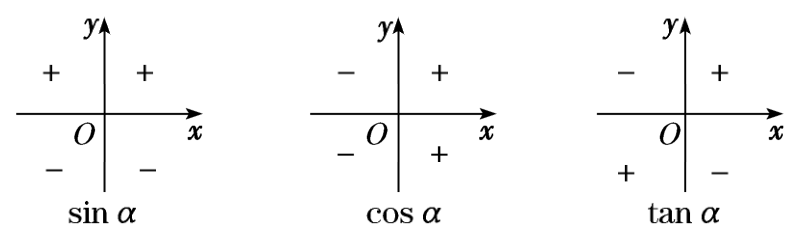
| 象限角 / 轴线角 α | α 的范围 | sinα=ry
(α∈R) | cosα=rx
(α∈R) | tanα=xy
(α∈{α∣α=2π+kπ,k∈Z}) |
|---|
| 第一象限角 | (0,2π) | + | + | + |
| 第二象限角 | (2π,π) | + | − | − |
| 第三象限角 | (π,23π) | − | − | + |
| 第四象限角 | (23π,2π) | − | + | − |
| 终边在 x 轴非负半轴 | α=0 | 0 | 1 | 0 |
| 终边在 y 轴非负半轴 | α=2π | 1 | 0 | 无定义 |
| 终边在 x 轴非正半轴 | α=π | 0 | −1 | 0 |
| 终边在 y 轴非正半轴 | α=23π | −1 | 0 | 无定义 |
可以简记为「CAST」,即在第四、一、二、三象限为正的三角函数分别为 Cos,“All”,Sin,Tan.
正弦函数 y=sinx、余弦函数 y=cosx、正切函数 y=tanx 为高中涉及到的三角函数.
*此外还有三个三角函数,高中不要求掌握:
- 余割函数 y=cscx=sinx1;
- 正割函数 y=secx=cosx1;
- 余切函数 y=cotx=tanx1.