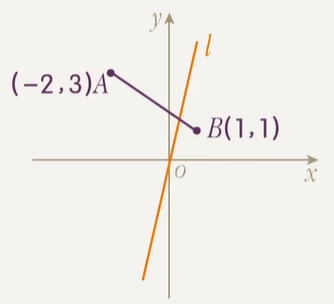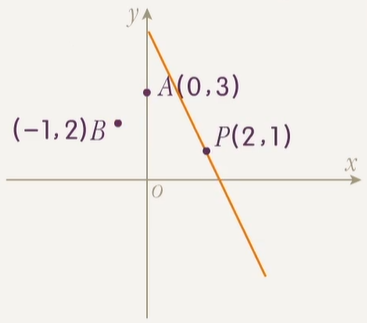在向量中我们学习过,一个点和一个 非零向量 可以确定一条直线,该向量称作直线的 方向向量.
一条直线的方向向量一定不唯一,设 s 是直线 l 的方向向量,则与 s 平行的所有 非零向量 都是 l 的方向向量,与 s 不平行的向量或零向量则均不为 l 的方向向量.
在学习直线这一节时,我们要有意识地将量化直线方向的工具在一起记忆.上面的方向向量就是我们第一个了解到的量化直线方向的工具,接下来我们再引入两个量化直线方向的工具:斜率和倾斜角.
对于一条直线 l,它的 倾斜角 定义如下:
- 如果 l 和 x 轴相交于一点 A,从 A 出发,沿着 l 的向上方向,沿着 x 轴正向 分别作出两条射线,这两条射线之间的夹角 α 即为 l 的倾斜角.这种情况下,0<α<π.
- 否则,l 要么和 x 轴平行,要么和 x 轴重合.此时规定 l 的倾斜角为 0.
提示:相交只包含两直线交于 恰好一点 的情况,即 重合不是相交.
因此一条直线 l 的倾斜角 α 的取值范围是 [0,π).
下面给出倾斜角的示例图:

上图中的 α1,α2,α3,α4 分别是 l1,l2,l3,l4 的倾斜角.
一条直线的倾斜角只有一个,如 α3 的补角就不是 l3 的倾斜角.
倾斜角必须是 l 的 向上方向 和 x 轴 正向 形成的夹角.
量化同一方向时,不同的量化方向工具之间应当具有关联.下探究任意直线 l 的方向向量与倾斜角的关系.
取 l 的一个 纵坐标非负 的方向向量 s=(x,y).这一定可以做到:任取 l 的一个方向向量,若其纵坐标为负,取该向量的相反向量即可.
设 x 轴正方向单位向量为 i=(1,0),l 的倾斜角为 θ,根据倾斜角的定义,有
⟨s,i⟩=θ
根据三角函数的定义,当 x=0 时,
tan(⟨s,i⟩)=xy
可得
tanθ=xy
对于 x=0 的情形,其倾斜角的正切不存在,倾斜角本身等于 2π,为一条 竖直线.
因此,量化同一方向时:
- 对于 非竖直线,倾斜角的正切等于任一方向向量的纵坐标与横坐标的比.
- 对于 竖直线,倾斜角的正切不存在,任一方向向量横坐标为 0.
在直线倾斜角的正切存在,即直线不竖直时,称 倾斜角的正切 为斜率.斜率常用小写字母 k 表示,即
k=tanα
规定竖直直线斜率不存在.
与斜率不同,一条直线的倾斜角总是存在的.
根据斜率的定义,斜率的存在性和倾斜角的正切保持同步,而不和倾斜角保持同步.
斜率与倾斜角的关系是显然的,因此斜率、倾斜角与方向向量三者可互化.
已知直线上不重合的两点的坐标,根据两点确定一条直线,方向也随之确定了.因此,量化方向的工具与直线上任意不重合两点的坐标应当也有联系.
对于直线 l 上不重合两点 (x1,y1) 和 (x2,y2),可导出 l 的一个方向向量 (x,y)=(x1−x2,y1−y2).这就建立了方向向量与两点坐标的联系.
因此,对于 非竖直线,
k=x1−x2y1−y2=tanα=xy
这个公式总结了三个量化直线方向的工具与两点坐标之间的关系,称作 斜率公式.
直线非竖直 是斜率公式的重要使用前提.对于不确定是否竖直的直线,使用斜率公式前,应讨论直线是否竖直(斜率是否存在).
当然,如果题意确定了直线的斜率存在(如题目条件「直线的斜率是 2」),就不必讨论了.另外,当题目中说「直线的斜率不为 0」这种表述时,也默认题目暗指直线斜率存在.
已知 l 经过 (a,a+4) 和 (2,2a+2) 两个不同的点,求 l 的倾斜角 α.
本题就是一个需要注意讨论的典型例题,如下:
若 l 的斜率存在,有 k=tanα=2−a(2a+2)−(a+4)=2−aa−2(斜率公式).因此 k=−1,α=43π.
若 l 的斜率不存在,有两点横坐标相同,即 a=2.此时两点纵坐标均为 6,即两点重合,与题意不符,舍去.
综上,α=43π.
根据 α∈[0,π) 可知,任意实数 k 作为斜率恰好有唯一的倾斜角 α 与之对应.
因此,l1,l2 方向相同,等价于 α1=α2,等价于 k1=k2 或斜率同时不存在;等价于 s1∥s2.
根据 k=tanα,令 α 从 0 开始逐渐增大,有:
- α 从 0 无限趋近 2π 的过程中,k 从 0 增大,无限趋近 +∞,增长速度越来越快.
- α 跨越 2π 的时候,k 从 +∞ 突变为 −∞.
- α 从 2π 到接近 π 的过程中,k 从 −∞ 增大,趋近于 0,增长速度越来越慢.
另外,∣k∣ 越大,直线的方向和 y 轴越接近,我们认为这个直线越「陡峭」.
斜率量化直线方向的优势在于:它是一种可以用全体实数量化绝大部分直线方向的工具(只有竖直方向无法量化,当然读者也可以认为斜率不存在也是一种变相量化竖直方向的方式).
已知直线 l 的斜率为 −tan7π,求 l 的倾斜角.
相当于已知 tanα=−tan7π 且 α∈[0,π),求 α.
不难发现 α=−7π+kπ,k∈Z,且落在 [0,π) 的只有一个值 76π.因此答案是 76π.
同时,有六个特殊角 6π,4π,3π,32π,43π,65π,请读者建立起它们和对应斜率值的映射,分别为 33,1,3,−3,−1,−33.
已知两点 A(−1,−5),B(3,−2),且一直线 l 倾斜角为直线 AB 的一半,求 l 的斜率.
设直线 l 的倾斜角为 α,则直线 AB 的倾斜角为 2α.根据倾斜角和两点坐标的关系,有 tan2α=−1−3−5−(−2)=43,而根据斜率和倾斜角的关系,我们要求的是 tanα.
现在问题变成 tan2α=43 求 tanα.根据倾斜角的范围,我们有 α∈[0,π) 且 2α∈[0,π),得 α∈[0,2π).
倍角公式展开 tan2α=1−tan2α2tanα=43,整理得 (3tanα−1)(tanα+3)=0,解得 tanα=31 或 tanα=−3.
根据 α∈[0,2π),有 tanα>0,因此 tanα=31.因此 l 的斜率是 31.
设某直线的斜率 k 满足 k∈(−1,1],求 α 的取值范围.
本质是已知 tanα∈(−1,1] 且 α∈[0,π),求 α 的取值范围.
三角函数已知函数值范围求角度范围,做法是先绘制函数图像再划线.绘制 tanα 在 [0,π) 上的图像和 y=1,y=−1 两条线:
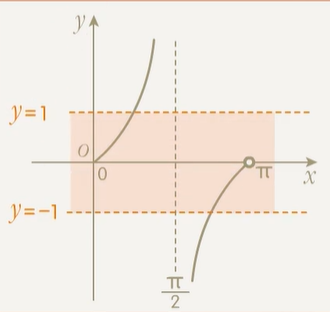
不难看出落在内部的 α 的范围应是 [0,4π]∪(43π,π).
这个比已知斜率范围求倾斜角范围简单,实质上就是已知角度范围求正切函数的值域.
读者足够熟悉正切函数的话,这种问题应当毫无难度,略过.
已知 A(−2,3),B(1,1),O 为坐标系原点.过 O 的直线 l 与线段 AB 相交,求 l 的斜率取值范围.
这种题目步骤比较固定,如下:
- 下设直线必经点为 P(例题 2.5.1 中这个 P 就是坐标系原点 O),线段的两个端点分别为 A 和 B.
- 分别作出 PA,PB 两条直线,并算出两条直线的斜率.
- 判断直线能取的范围是从 PA 逆时针扫到 PB 这个范围,还是能从 PB 逆时针扫到 PA 这个范围(钦定 逆时针 旋转是因为逆时针旋转时 α 增大,斜率也在分段增大,不易出错).
旋转过程中,有两个分段点需要注意:
- 直线 逆时针 扫过与 y 轴平行的线(称之为「竖直线」)时,斜率 从 +∞ 突变为 −∞,倾斜角不突变.
- 直线 逆时针 扫过与 x 轴平行的线(称之为「水平线」)时,倾斜角 从趋近 π 突变为 0,斜率不突变.
如果求斜率范围,注意「竖直线」为分段点;如果求倾斜角范围,注意「水平线」为分段点.
根据题目画图.
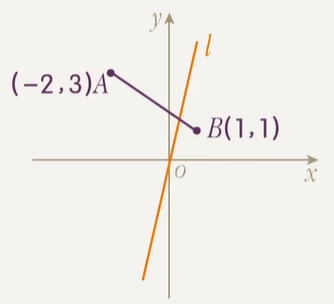
作出直线 OA,OB.不难发现 l 能扫过的范围是从 OB 逆时针扫到 OA 这一段,考虑其斜率变化.
计算可得 kOA=−23,kOB=1.
从 OB 逆时针转到 OA,斜率的变化是先从 1 增大到 +∞,经过「竖直线」后突变到 −∞,再增大到 −23.
综上,斜率的取值范围为 (−∞,−23]∪[1,+∞].
已知 l 过定点 (2,1),且点 A(3,0),B(−1,2) 位于直线 l 的同侧,求 l 的斜率取值范围.
根据题目画图.
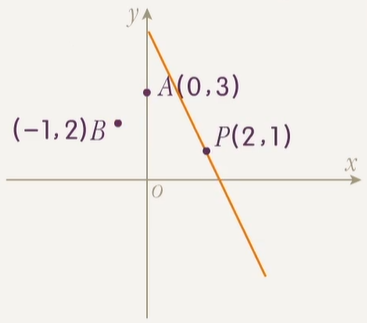
A 和 B 落在直线 l 的同侧,等价于 l 和线段 AB 不相交,l 的旋转范围是从 PB 逆时针转到 PA.
计算斜率 kPA=−1,kPB=−31.
整个过程中,斜率从 −31 一直增大到 +∞,转过竖直线后突变为 −∞,再增大到 −1.
因此答案是 (−∞,−1)∪(−31,+∞)(注意这里两个端点不能取,否则一个点落在直线上,不是同侧).
指的是形如 x1−x2y1−y2 的分式可以看成是 (x1,y1) 和 (x2,y2) 连线的斜率,从而利用数形结合解决问题.
已知 A(−3,0),B(0,−2),若点 P(x,y) 在线段 AB 上,求 x−1y−2 的取值范围.
将所求转化为求 P 和 (1,2) 连线的斜率范围,则问题变成:过定点 (1,2) 的直线和线段 AB 相交,求斜率范围.
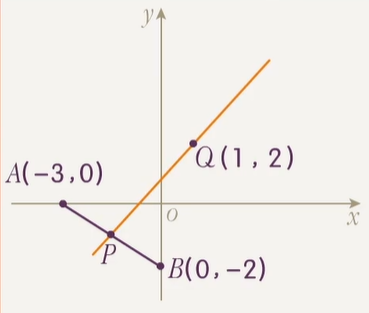
这就是过定点直线交于线段求斜率范围问题了,从 QA 逆时针转到 QB 不经过竖直线,因此答案是 [21,4].
已知 A(1,1),B(4,2),若点 P(x,y) 在线段 AB 上,求 3−xy 的取值范围.
3−xy=−x−3y,所求可以转化为 P 和 Q(3,0) 连线斜率的相反数.
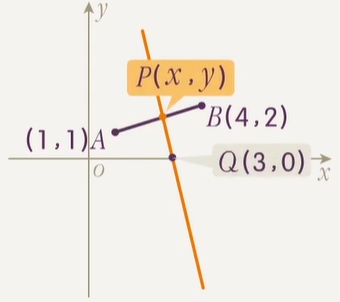
设 P 和 Q(3,0) 连线为 l,则 l 的范围为从 QB 逆时针转到 QA,经过竖直线.
从 QB 到竖直线斜率从 2 到 +∞,从竖直线到 QA 斜率从 −∞ 到 −21,因此斜率范围为 (−∞,−21]∪[2,+∞).
答案是斜率范围的相反数,为 (−∞,−2]∪[21,+∞).
上面这个例题中,出题人对斜率进行了变形.如果我们直接将 3−xy 看成斜率,结果是 (3,y) 和 (x,0) 连线的斜率,这样的信息明显难以使用.题目一般给定的 (x,y) 都是一个现成的动点坐标,所以我们一般将所求式子变形成 (x,y) 和某定点连线的斜率,从而解决问题.
上面出题人的变形仅仅是加了一个相反数.出题人还可以做很多变形,如:
- 倍乘:x−23y+3=(x−2)3(y+1)=3k.
- 倒数:y+12−x=−(x−2y+1)1=−k1(该例中还加了个负号).
事实上,分子与分母均为含 x,y 的 一次式 的 分式 均可以考虑转成斜率(运用分离常数和取倒数技巧),是一个比较常用的思想,值得注意.
「刻画几何条件」,就是将一个陌生的几何条件 P 等价 为一个容易处理的几何条件 Q.
这么做的目的是:
- 当题目的条件中出现几何条件 P 时,我们可以把这个条件直接等价为容易处理的几何条件 Q,从而解决题目.
- 当题目的结论是几何条件 P 时,我们可以转而证明几何条件 Q.
举例说明.比如后面会学习到「A,B,C 三点共线」等价为「AB 和 AC 方向相同」.这就是一个几何条件的刻画方式.那么在题目中:
- 如果题目的条件是「A,B,C 三点共线」,我们可以把这个条件等价为「AB 和 AC 方向相同」,再做题.
- 如果题目要求证明「A,B,C 三点共线」.我们可以转而去证明「AB 和 AC 方向相同」.
不同的刻画方式可能具有不同的解题效果.在后面的学习中,将会介绍很多常见的几何条件的通常最合适的刻画方式,便于读者做题的效率和正确率兼备.
先给出结论,对于两条可能重合的直线 l1,l2,有如下的等价关系:
| 位置关系 | 方向向量意义上的等价 | 倾斜角意义上的等价 | 斜率意义上的等价(要求 l1,l2 斜率存在) |
|---|
| l1∥l2 | a1∥a2
且 l1,l2 不重合 | α1=α2
且 l1,l2 不重合 | k1=k2
且 l1,l2 不重合 |
| l1 和 l2 相交 | a1∦a2 | α1=α2 | k1=k2 |
| l1⊥l2 | a1⊥a2 | ∣α1−α2∣=2π | k1k2=−1 |
同一行的四个条件互相等价.这些结论都可以直接使用.
当
k1,
k2 存在时,
l1⊥l2⟺k1k2=−1 的证明
考虑分别提取 l1 和 l2 的一个方向向量 (1,k1) 和 (1,k2),有 (1,k1)⋅(1,k2)=0,即 k1k2+1=0.
下面是几点说明:
- 平行总是等价于方向相同 且不重合.这一步「平行的判重」非常重要.
- 两直线垂直时的 ∣α1−α2∣=2π,只要 α1 唯一确定,则 α2 也唯一确定.具体来说,
- α1∈[0,2π) 时,α2=α1+2π.
- α1∈[2π,π) 时,α2=α1−2π.
等价刻画「l1 和 l2 重合」的两种方式:
- l1 和 l2 方向相同 并且 经过同一个点(一个点和一个方向确定一条直线).
- l1 的方程和 l2 的 方程等价.
一种等价刻画「A,B,C 三点共线」的方式是:直线 AB 和直线 AC 的方向相同.即 从三点中的一点出发,向另外两点连线,连线方向相同与三点共线等价.
证明这个刻画的等价性.如果直线 AB 和直线 AC 方向相同,则又因为它们经过同一点 B,直线 AB 和 AC 重合.那么点 B 在直线 AB 上的同时,也一定在直线 AC 上.同时,点 A 和点 C 也在直线 AC 上,因此 A,B,C 三点共线.
而如果 A,B,C 三点共线,显然直线 AB 和直线 AC 的方向相同.所以上面的刻画等价.
先前讲到,两直线平行的一种等价刻画方式为:两直线方向相同且证明两直线不重合.两直线不重合如何进一步刻画?
要证明 l1 和 l2 不重合:
- 当方程可知,可以证明 l1 和 l2 方程不等价.
- 否则,可以在两直线上各取一点连线,证明该线的方向不同于两直线中的某一条.
两条直线方向向量和夹角的关系,可直接使用向量夹角的知识求解.下面讨论夹角和倾斜角与斜率的关系,并引入一个新概念:到角.
两相交直线的 夹角(两直线所成角) 的定义为:两直线所成的两对对顶角中,较小 的一对角中,其中一个的大小.
一条直线 l1 到另一条相交直线 l2 的 到角 的定义为:l1 沿着与 l2 的唯一交点 逆时针旋转 到第一次与 l2 重合时的旋转角.将 l1 称作到角的 始边,l2 称作到角的 终边.
对于平行或重合的直线,认为它们不存在夹角和到角.
- l1 到 l2 的到角为 锐角或直角 时,它就是 l1 和 l2 的夹角.
- l1 到 l2 的到角为 钝角 时,它是 l1 和 l2 夹角的 补角.
- 到角的范围是 (0,π),而夹角的范围是 (0,2π].
对于任意一个角 α,{β∈[0,π)∣β+kπ,k∈Z} 恰有唯一元素 β,记 β=αmodπ.
两直线 到角 与 倾斜角 的关系:l1 倾斜角为 α,l1 到 l2 的到角为 θ,则 l2 倾斜角为 (α+θ)modπ.
两直线 夹角 与 倾斜角 的关系:l1 倾斜角为 α,l1 与 l2 的夹角为 θ,则 l2 的倾斜角为 (α+θ)modπ 或 (α−θ)modπ,对应 l1 到 l2 的到角分别为 θ 和 π−θ.
上面是两直线到角和夹角和两直线倾斜角之间的关系,现试探究两直线到角和夹角和两直线斜率之间的关系.
当 l1 到 l2 的到角为 θ 时,我们有 θ=(α2−α1)modπ.当 θ=2π 且 α1=2π 且 α2=2π 时,有:
tanθ=tan[(α2−α1)modπ]=tan(α2−α1)=1+tanα1tanα2tanα2−tanα1=1+k1k2k2−k1
也即 l1 到 l2 的到角为 θ 时,tanθ=1+k1k2k2−k1.这条结论称作 到角公式,它给出了一直线到另一直线的到角和两直线斜率的关系.注意分子上是 终边的斜率减去始边的斜率,不能反.
当 l1 和 l2 的夹角为 θ 时,l1 到 l2 的到角为 θ 或 π−θ.当 θ=2π 且 α1=2π 且 α2=2π 时,我们有 θ∈(0,2π),此时 tanθ>0,tan(π−θ)<0.
- 当 l1 到 l2 的到角为 θ 时,有 tanθ=∣tanθ∣=1+k1k2k1−k2.
- 当 l1 到 l2 的到角为 π−θ 时,有 tanθ=−tan(π−θ)=∣tan(π−θ)∣=1+k1k2k1−k2.
综上 l1 和 l2 的夹角为 θ 时,tanθ=1+k1k2k1−k2.这条结论称作 夹角公式,也即到角公式上套一个绝对值,这时分子相减的顺序不重要.
需要注意的是,到角公式和夹角公式并不是课本上公式,不要在大题中使用.
到角公式和夹角公式的使用前提:两直线斜率均存在且夹角不为直角.
给定 l1,l2 的方向信息(为方向向量、倾斜角、斜率、两点坐标中的一种),求 l1 与 l2 的位置关系.
- 如果两直线给出的方向信息为 同一种(如均为倾斜角),直接套用上面讲过的结论即可.
- 如果 不是同一种,将两直线的方向信息都 统一成斜率 再做.这就是统一斜率原则.
为什么要选择统一成斜率?因为无论是已知了直线的方向向量,还是倾斜角,还是不重合的两点坐标,算出斜率都是很简单的.如果斜率存在,方向向量直接将坐标比一下即可,倾斜角直接正切一下即可,不重合两点坐标直接代入斜率公式即可.
而倾斜角无论是从斜率,从两点坐标,还是从方向向量,都需要一个「逆正切函数」的过程;而方向向量从倾斜角得到也必须先转成斜率.综上,统一成斜率一般是最简单的.
另外如果两直线给出的方向信息为同一种,但都是两点坐标时,也要统一成斜率做.原因很简单,并没有「直线上两点坐标」和「直线位置关系」之间关系的直接结论.
需要特别注意 平行的验重 和 斜率不存在 两种容易遗漏的情况.
已知直线位置关系求参数,可以沿用上面的策略:将两直线的方向统一成斜率表示.
具体来说,我们可以将两直线的斜率表示成带参数的式子,然后再根据已知的直线位置关系列出两个斜率应该满足的式子,从而解出参数 k.
注意事项还是平行的验重和斜率公式的使用前提,判断斜率是否存在.
已知过 A(m,1),B(−1,m) 两点的直线 l1 和过 P(1,2),Q(−5,0) 两点的直线 l2 平行,求 m 的值.
l2 存在斜率 k2=1−(−5)2−0=31.因此,l1 的斜率必须存在且等于 l2 的斜率,即 k1=31.
m 取什么值都不能使 A,B 两点重合.根据斜率公式,有 m−(−1)1−m=31,解得 m=21.
现验证 m=21 时 l1 和 l2 不重合.因为 kAP=1−212−1=2=k2,所以 l1 和 l2 不重合.
已知过 A(m,1),B(−1,m) 两点的直线 l1 和过 P(1,2),Q(−5,0) 两点的直线 l2 垂直,求 m 的值.
l2 存在斜率 k2=1−(−5)2−0=31.因此,l1⊥l2 等价于 l1 的斜率存在且 k1k2=−1.
m 取什么值都不能使 A,B 两点重合.根据斜率公式,有 k1=m−(−1)1−m,于是有 m−(−1)1−m⋅31=−1,解得 m=−2.
若正方形一条对角线所在直线斜率为 2,求该正方形两条邻边所在直线的斜率分别是多少.(填空题)
正方形两条邻边分别和对角线呈 4π 的夹角.设对角线所在直线倾斜角为 α,根据 tanα=2,不难发现有 α∈(4π,2π),因此两邻边所在直线的倾斜角分别为 α−4π 和 α+4π.
现在要求两邻边所在直线的斜率,即 tan(α−4π) 和 tan(α+4π).以计算 tan(α+4π) 为例,用正切和角展开为 1−tanαtan4πtanα+tan4π,将 tanα=2 代入可得结果为 −3.同理可得另外一个结果为 31.
计算可以更快:注意到正方形两邻边垂直,其所在直线斜率互为负倒数.所以将一个直线的斜率算出来后,另一个直线斜率采负倒数即可.
显然所求的两直线以及对角线所在直线斜率存在,且对角线和所求直线夹角不为直角,可以使用夹角公式.
设所求直线斜率为 k,则 k 应当满足 1+2k2−k=1,两解分别为 −3 和 31,就是所求的两直线斜率.