两个距离公式

公式内容

点到直线的距离

对于点 $P(x_0, y_0)$ 和直线 $l$：$Ax + By + C = 0$，下探究 $P$ 到 $l$ 的距离．

设 $l$ 上任意一点 $Q(x_1, y_1)$，则 $P$ 到 $l$ 的距离等于 $\overrightarrow{PQ} = (x_1 - x_0, y_1 - y_0)$ 向 $l$ 的法向量方向 $(A, B)$ 的 投影 的 绝对值，即

$$\df{\lv (x_1 - x_0, y_1 - y_0) \cdot (A, B)\rv}{\lv (A, B)\rv}$$

分母 $\lv (A, B) \rv = \sqrt{A^2 + B^2}$，对分子进行推导：

$$\lv (x_1 - x_0, y_1 - y_0) \cdot (A, B)\rv = \lv A(x_1 - x_0) + B(y_1 - y_0)\rv = \lv \red{Ax_1 + By_1 + C} - Ax_0 - By_0 - C\rv$$

因为 $Q(x_1, y_1)$ 在 $Ax + By + C = 0$ 上，标红的式子为 $0$，因此分子最终可简化为

$$\lv Ax_0 + By_0 + C \rv$$

因此，点 ${P(x_0, y_0)}$ 到直线 $l$：${Ax + By + C = 0}$ 的距离为 ${\df{\lv Ax_0 + By_0 + C\rv}{\sqrt{A^2 + B^2}}}$．该结论可以直接使用．

上面直线 $l$ 采用一般式是因为它是唯一能涵盖所有直线的情况，并且一般式推出的距离公式形式比较优美．遇到用其它形式表示的直线时，将直线方程变形为一般式形式再套用点到直线距离公式即可．如下：

例题 1.1

求 $(-2, 1)$ 到 $y = \df 1 3 x - 5$ 的距离．

例题 1.1 解答

直线方程等价于 $x - 3y - 15 = 0$．距离 $d = \df{|1 \times(-2) - 3 \times 1 - 15|}{\sqrt{1^2 + (-3)^2}} = 2\sqrt{10}$．

当然，足够特殊的直线，如水平横线和竖直线，点到直线距离都只是两个坐标的差，就没必要套用上面的公式了．

平行线间距离

对于两条平行线 $l_1$：$Ax + By + C_1= 0$ 和 $l_2$：$Ax + By + C_2 = 0$，这里 $C_1 \ne C_2$，探究它们的距离．

可以在 $l_1$ 上任取一点 $P(x_0, y_0)$，则 $P$ 到 $l_2$ 的距离就是两直线间距离：

$$\df{\lv Ax_0 + By_0 + C_2\rv}{\sqrt{A^2 + B^2}} = \df{\lv \red{Ax_0 + By_0 + C_1} + C_2 - C_1\rv}{\sqrt{A^2 + B^2}} = \df{\lv C_1 - C_2\rv}{\sqrt{A^2 + B^2}}$$

标红的式子为 $0$ 是因为 $P(x_0, y_0)$ 在 $Ax + By + C_1 = 0$ 上．

因此，两条平行线 ${l_1}$：${Ax + By + C_1= 0}$ 和 ${l_2}$：${Ax + By + C_2 = 0}$ 之间的距离为 ${\df{\lv C_1 - C_2\rv}{\sqrt{A^2 + B^2}}}$．该结论可以直接使用．

对于 $x$ 和 $y$ 系数不等，但对应成比例的直线，显然它们也平行，将系数统一后代入求解公式即可．下面是一个例子：

例题 1.2

求 $3x + 4y - 9 = 0$ 和 $6x + 8y +3 = 0$ 的距离．

例题 1.2 解答

统一系数为 $6x + 8y - 18 = 0$ 和 $6x + 8y + 3 = 0$．

距离 $d = \df{|-3 - 18|}{\sqrt{6^2 + 8^2}} = \df{21}{10}$．

直线综合大题

至此，所有教材上出现过的，有关直线和点几何条件的刻画方式已经全部讲解完毕．但在实际做题时，还会见到许多有关直线和点的陌生的几何条件，此时我们就要设法将它们等价为我们熟悉的，会刻画的几何条件，从而解决问题．

如「$P$ 和 $Q$ 关于直线 $l$ 对称」就是一个陌生的几何条件，但我们可以等价为「$PQ \perp l$」和「$PQ$ 的中点在 $l$ 上」两个几何条件，这两个条件我们都是会刻画的．

本章将会总结一些非常经典的几何条件（如上面提到的对称），并给出这些几何条件通常最简单的刻画方法．这类问题比较常见，请读者熟练掌握．

有时可以考虑几何

例题 2.1

一直线 $l$ 过点 $P(1, 2)$，且与 $M(2, 3)$ 和 $N(4, -5)$ 的距离相等，求 $l$ 的方程．

例题 2.1 代数法解答

（$l$ 为已知过一点 + 其它信息形式，列成斜率为参数的点斜式．勿忘分类讨论．）

当 $l$ 斜率不存在时，$l$ 为 $x = 1$，不符要求，舍去．

当 $l$ 斜率存在时，设 $l$ 方程为 $y - 2 = k(x - 1)$．为方便计算距离，变形为一般式形式 $kx - y - k + 2 = 0$．

$l$ 到 $M$ 距离为 $\df{|2k - 3 - k + 2|}{\sqrt{k^2 +1}} = \df{|k - 1|}{\sqrt{k^2 +1}}$，$l$ 到 $N$ 距离为 $\df{|4k + 5 - k + 2|}{\sqrt{k^2 + 1}} = \df{|3k + 7|}{\sqrt{k^2 +1}}$．

两距离相等，即 $\df{|k - 1|}{\sqrt{k^2 +1}} = \df{|3k + 7|}{\sqrt{k^2 +1}}$，解得 $k = -4$ 或 $k = -\df 3 2$．

因此，直线 $l$ 的方程为 $4x + y - 6 = 0$ 或 $3x + 2y - 7 = 0$．

例题 2.1 几何法解答

$l$ 到 $M$ 和 $N$ 的距离相等，只有两种情况：$l \parallel MN$，或者 $l$ 经过 $MN$ 中点．

第一种情况可以知道 $l$ 过一点（已知条件的 $(1, 2)$）和斜率（与 $MN$ 平行），点斜式直接求得 $4x + y - 6 = 0$．

第二种情况可以知道 $l$ 过两点（已知条件的 $(1, 2)$ 和 $MN$ 中点），先算斜率再点斜式直接求得 $3x + 2y - 7 = 0$．

可以看到，几何法的计算量明显少于代数，效率更高．但是几何法的两种情况容易漏掉其中一种导致丢解，因此代数法相对更稳定．读者可以根据自己的喜好和实际情况选择适合自己的方法．

点到直线的垂足

点到直线的垂足 标准做法

求点 $P(x_0, y_0)$ 到直线 $l$：$Ax + By + C = 0$ 的垂足 $H$ 的坐标．

最简单的做法是：计算出 $l$ 的斜率，从而计算出垂线 $PH$ 的斜率．

根据垂线 $PH$ 的斜率和点 $P$ 的坐标列点斜式，为直线 $PH$ 的方程．与 $l$ 的方程联立即得到 $H$ 的坐标．

例题 2.2

若点 $P(1, 3)$ 到直线 $l$：$y = -3x - 4$ 的垂足为 $H$，求 $H$ 的坐标．

例题 2.2 解答

$l$ 的斜率为 $-3$，则 $PH$ 的斜率为 $\df 1 3$，直线 $PH$ 方程为 $y - 3 = \df 1 3 (x - 1)$．

与 $y = -3x - 4$ 联立解得 $\begin{cases}x = -2 \\ y = 2\end{cases}$．$H$ 的坐标为 $(-2, 2)$．

点到直线的垂足 选填速算技巧

求点 $P(x_0, y_0)$ 到直线 $l$：$Ax + By + C = 0$ 的垂足 $H$ 的坐标．

有结论：$H$ 的坐标就是 $P$ 的坐标 减去 向量 $t(A, B)$，其中 $t = \df{Ax_0 + By_0 +C}{A^2 + B^2}$．

注意到 $t$ 和点到直线的距离公式很像，但有两个差别：一是分子不再有绝对值；二是分母不再有根号．

点到直线的垂足 速算技巧证明

考虑 $\overrightarrow{OH} = \overrightarrow{OP} + \overrightarrow{PH}$．所求的 $H$ 的坐标实际就是 $\overrightarrow{OH}$，$\overrightarrow{OP}$ 也即已知 $P$ 的坐标．我们只需求出 $\overrightarrow{PH}$．

因为 $PH \perp l$，所以 $\overrightarrow{PH}$ 是 $l$ 的一个法向量，且模长应等于 $P$ 到 $l$ 距离，即 $\df{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$．

我们取 $l$ 的法向量 $(A, B)$，它的模长为 $\sqrt{A^2 + B^2}$．记 $t = \df{Ax_0 + By_0 +C}{A^2 + B^2}$，则 $t(A, B)$ 的模长与 $P$ 到 $l$ 的距离相同．于是，$t(A, B)$ 就是一个与所求向量 $\overrightarrow{PH}$ 平行且大小相等的向量，因此 $t(A, B)$ 要么是 $\overrightarrow{PH}$ 要么是 $\overrightarrow{HP}$，现确定 $t(A, B)$ 的方向．

设 $H(x_1, y_1)$，我们有：

$$\begin{aligned} t(A, B) \cdot \overrightarrow{HP} &= t[(A, B) \cdot \overrightarrow{HP}] \\ & = t[(A, B) \cdot (x_0 - x_1, y_0 - y_1)] \\ & = t[A(x_0 - x_1) + B(y_0 - y_1)] \\ & = t(Ax_0 + By_0 + C - Ax_1 - By_1 - C) \\ & = t(Ax_0 + By_0 + C) \\ & = \df{Ax_0+By_0+C}{A^2 + B^2} \times (Ax_0 + By_0 + C)\\ & = \df{(Ax_0+By_0+C)^2}{A^2 + B^2} > 0 \end{aligned}$$

这证明了 $t(A, B)$ 和 $\overrightarrow{HP}$ 是同向的，说明 $t(A, B) = \overrightarrow{HP}$．我们构造它的相反向量 $-t(A, B)$，就是 $\overrightarrow{PH}$ 了．

因此 $Q$ 的坐标就是 $P$ 的坐标加上 $-t(A, B)$，即减去 $t(A, B)$．

例题 2.2

若点 $P(1, 3)$ 到直线 $l$：$y = -3x - 4$ 的垂足为 $H$，求 $H$ 的坐标．

例题 2.2 解答（技巧）

将 $l$ 的方程变形为 $3x + y + 4 = 0$，根据 $P(1, 3)$，算出 $t$ 值为 $\df{3 \times 1 + 3 + 4}{3^2 + 1^2} = 1$．

于是垂足坐标为 $(1, 3) - t(3, 1) = (-2, 2)$．

点到直线的垂足 特殊情况 1

求点 $P(x_0, y_0)$ 到 $l$ 的垂足 $H$ 的坐标，其中 $l$ 为水平线或竖直线．

点 $P(x_0, y_0)$ 到直线 $x = x_1$ 的垂足为 $(x_1, y_0)$；到直线 $y = y_1$ 对称的点为 $(x_0, y_1)$．

结论可以直接使用．

点到直线的垂足 特殊情况 2 选填速算技巧

求点 $P(x_P, y_P)$ 到 $l$：$Ax + By + C = 0$ 的垂足坐标，其中 $l$ 的斜率为 ${\pm 1}$，即 ${|A| = |B|}$．

参见 点关于直线对称 特殊情况 2 选填速算技巧，这种情况下我们可以快速的计算出 $P$ 的对称点 $P'$．然后，我们算出 $P$ 和 $P'$ 的中点，就是所求垂足的坐标．

点关于点对称

接下来几节考虑讨论刻画对称．

点 $P(x, y)$ 与点 $Q$ 关于 $A(x_0, y_0)$ 对称，求 $Q$ 的坐标．

已知等价于 $A$ 是 $PQ$ 的中点．因此，我们有 $Q = (2x_0 - x, 2y_0 - y)$．

直线关于点对称

直线关于点对称 标准做法

求 $l_1$：$Ax + By + C = 0$ 关于点 $P(x_0, y_0)$ 对称的直线 $l_2$ 的解析式．

计算量最小的标准做法是：将已知等价于下面两个条件：

• $l_2 \parallel l_1$（使用平行直线系列出 $l_2$ 的含参方程）．
• 在 $l_1$ 上取一点 $Q$，将 $Q$ 沿 $P$ 对称为 $Q'$ 后，$Q'$ 在 $l_2$ 上（进一步求出参数）．

例题 2.4

求 $2x + 3y + 16 = 0$ 关于点 $P(0, 1)$ 对称的直线方程．

例题 2.4 解答

对称的直线和原直线平行，设对称的直线为 $2x + 3y + m = 0$．

考虑原直线上任意一点 $(-8, 0)$，关于点 $P(0, 1)$ 对称后的点为 $(8, 2)$．$(8, 2)$ 在 $2x + 3y + m = 0$ 上，解得 $m = -22$．

因此对称后的直线方程为 $2x + 3y - 22 = 0$．

直线关于点对称 选填速算技巧

求 $l_1$：$Ax + By + C = 0$ 关于点 $P(x_0, y_0)$ 对称的直线 $l_2$ 的解析式．下面是一个技巧做法．

第一步：根据平行直线系列出 $l_2$ 的方程：$Ax + By + m = 0$．

第二步：将 $l_1$ 和 $l_2$ 两个方程相加，得到 $Ax + By + C + Ax + By + m = 0$．

第三步：可以证明 $P$ 的坐标满足上面那个方程，即 $Ax_0 + By_0 + C + Ax_0 + By_0 + m = 0$ 成立，可解出 $m$．

直线关于点对称速算技巧证明

只需证明 $P$ 的坐标满足方程 $Ax + By + C +Ax + By + m = 0$．

$l_1$ 和 $l_2$ 关于 $P$ 对称，还等价于 $l_1 \parallel l_2$ 且 $P$ 到 $l_1$ 的距离等于 $P$ 到 $l_2$ 的距离．即

$$\df{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}} = \df{|Ax_0 + By_0 + m|}{\sqrt{A^2 + B^2}}$$

于是

$$|Ax_0 + By_0 + C| = |Ax_0 + By_0 + m|$$

因为 $m \ne C$，所以左右两个绝对值内部的值不能相等，只能互为相反数，相加为 $0$，证毕．

例题 2.4

求 $2x + 3y + 16 = 0$ 关于点 $P(0, 1)$ 对称的直线方程．

例题 2.4 解答（技巧）

列方程：$2 \times 0 + 3 \times 1 + 16 + 2 \times 0 + 3 \times 1 + m = 0$，直接解出 $m = -22$．

所以直线方程为 $2x + 3y - 22 = 0$．

这个技巧做法不能在大题中直接使用，想用还需要证明一遍，效率反而不如标准做法．不过选填中这个技巧还是快于标准做法的．

点关于直线对称

点关于直线对称 标准做法

求点 $P(x_0, y_0)$ 关于 $l$：$Ax + By + C = 0$ 对称的点 $Q$ 的坐标．

计算量最小的标准做法是：将对称条件等价为下面两个条件：

• $PQ \perp l$．
• $PQ$ 的中点在 $l$ 上．

设 $Q$ 的坐标为 $(x_Q, y_Q)$，上面两个条件分别转成两个方程，可以解出 $x_Q$ 和 $y_Q$．

例题 2.5.1

若点 $P(1, 3)$ 和 $Q$ 关于直线 $y = -3x - 4$ 对称，求 $Q$ 的坐标．

例题 2.5.1 解答

设 $Q$ 的坐标为 $(x_Q, y_Q)$．对称等价于：

• $PQ \perp l$．即 $PQ$ 的斜率存在且为 $-3$ 的负倒数 $\df{1}3$．根据斜率公式有 $\df{y_Q - 3}{x_Q - 1} = \df 1 3$．
• $PQ$ 的中点在 $l$ 上．即 $(\df{1 + x_Q}2, \df{3 + y_Q}2)$ 在 $l$ 上，即 $\df{3 +y_Q}2 = -3 \times \df{1+x_Q}2 - 4$．

联立两个方程解得 $\begin{cases}x_Q = -5 \\ y_Q = 1\end{cases}$，即 $Q(-5, 1)$．

点关于直线对称 选填速算技巧

求点 $P(x_0, y_0)$ 关于 $l$：$Ax + By + C = 0$ 对称的点 $Q$ 的坐标．

有结论：$Q$ 的坐标就是 $P$ 的坐标减去向量 $2t(A, B)$，其中 $t = \df{Ax_0 + By_0 +C}{A^2 + B^2}$．这个 $t$ 和点到直线的垂足中的 $t$ 是同一个．

相信聪明的读者已经看出这个结论的道理了：$P - t(A, B)$ 得到垂足 $H$，而 $H$ 是 $PQ$ 的中点，自然而然地，$P$ 减去 $2$ 倍的 $t(A, B)$ 就得到对称点坐标了．

例题 2.5.1

若点 $P(1, 3)$ 和 $Q$ 关于直线 $y = -3x - 4$ 对称，求 $Q$ 的坐标．

例题 2.5.1 解答（技巧）

将直线变形为一般式方程 $3x + y + 4 = 0$．可算出 $t = \df{3 \times 1 + 3 + 4}{3^2 + 1^2} = 1$．

于是 $Q = P - 2t(3, 1)$，即 $(-5, 1)$．

点关于直线对称 特殊情况 1

求点 $P(x_0, y_0)$ 关于 $l$ 对称的点 $Q$ 的坐标，其中 $l$ 为水平线或竖直线．

点 $P(x_0, y_0)$ 关于直线 $x = x_1$ 对称的点为 $Q(2x_1 - x_0, y_0)$．原因是可以转化为关于点 $(x_1, y_0)$ 对称．

点 $P(x_0, y_0)$ 关于直线 $y = y_1$ 对称的点为 $Q(x_0, 2y_1 - y_0)$．原因是可以转化为关于点 $(x_0, y_1)$ 对称．

结论可以直接使用．

点关于直线对称 特殊情况 2 选填速算技巧

求点 $P(x_P, y_P)$ 关于 $l$：$Ax + By + C = 0$ 对称的点 $Q$ 的坐标，其中 $l$ 的斜率为 ${\pm 1}$，即 ${|A| = |B|}$．

在这种条件下有一个结论：设 $Q(x_Q, y_Q)$，则 $(x_P, y_Q)$ 和 $(y_P, x_Q)$ 都满足 $l$ 的方程．

结论证明

以 $PQ$ 为对角线作一个正方形．

因为 $PQ \perp l$，$l$ 的斜率为 $\pm 1$，因此 $PQ$ 的斜率为 $\mp 1$．这样以来，作出的正方形是一个与坐标轴平行，横平竖直的正方形，因此正方形除了 $PQ$ 的另外两个顶点坐标分别为 $(x_P, y_Q)$ 和 $(y_P, x_Q)$．

同时，这个正方形的一条对角线为 $PQ$，另外一条对角线所在直线恰好为 $l$．因此 $(x_P, y_Q)$ 与 $(y_P, x_Q)$ 在 $l$ 上，证毕．

所以我们可以将 $x_P$ 的值代入 $l$ 的方程，求出的 $y$ 值就是 $y_Q$；再将 $y_P$ 的值代入 $l$ 的方程，求出的 $x$ 值就是 $x_Q$．该结论同样不能在大题中直接使用．

例题 2.5.2

求 $(-2, 3)$ 关于直线 $y - x + 1 = 0$ 的对称点．

例题 2.5.2 解答

将 $x = -2$ 代入方程，得到 $y = -3$，为对称点的纵坐标．

将 $y = 3$ 代入方程，得到 $x = 4$，为对称点的横坐标．

因此对称点坐标为 $(4, -3)$．

这个特例下还有两个更特殊的例子：关于 $y = x$ 和 $y = -x$ 对称．

• $(x_0, y_0)$ 关于 $y = x$ 的对称点为 $(y_0, x_0)$．
• $(x_0, y_0)$ 关于 $y = -x$ 的对称点为 $(-y_0, -x_0)$．

直线关于直线对称

直线关于直线对称 情况 1：目标直线和对称轴平行

求 $l_1$：$Ax + By + C_1 = 0$ 关于 $l_2$：$Ax + By + C_2 = 0$ 对称的直线 $l_3$ 的方程，保证 $C_1 \ne C_2$．上面的方程已经保证了 $l_1 \parallel l_2$．

给定的对称关系可以等价为：$l_3$ 与 $\red{l_1}$ 平行，且 $l_3$ 到 $l_2$ 的距离等于 $l_1$ 到 $l_2$ 的距离．

注意：不能等价为与 $l_2$ 平行，因为必须排除 $l_3$ 和 $l_1$ 重合的可能．

设 $l_3$ 方程为 $Ax + By + C_3 = 0$（$C_3 \ne C_1$）．我们有：

$$\df{|C_3 - C_2|}{\sqrt{A^2 +B^2}} = \df{|C_1 - C_2|}{\sqrt{A^2 +B^2}}$$

即

$$|C_3 - C_2| = |C_1 - C_2|$$

因为 $C_3 \ne C_1$，绝对值内部的值无法相等，只能相反，即

$$C_3 - C_2 = C_2 - C_1$$

即 $C_3 = 2C_2 - C_1$．

例题 2.6.1

求直线 $l_1$：$2x + 3y - 1 = 0$ 关于直线 $l_2$： $4x + 6y + 4 = 0$ 对称的直线 $l_3$ 的方程．

例题 2.6.1 解答

$l_2$ 方程变形为 $2x + 3y + 2 = 0$，与 $l_1$ 的 $x$，$y$ 系数统一．设 $l_3$ 方程为 $2x + 3y + m = 0$（$m \ne -1$）．

$l_3$ 到 $l_2$ 的距离等于 $l_1$ 到 $l_2$ 的距离，即 $\df{|m - 2|}{\sqrt{2^2 + 3^2}} = \df{3}{\sqrt{2^2 + 3^2}}$，可得 $|m - 2| = 3$，即 $m = 5$（$-1$ 舍去）．

综上 $l_3$ 的方程为 $2x + 3y + 5 = 0$．

上面的解答按照标准过程的规范书写．在选填中，我们直接按照 $2 \times 2 - (-1) = 5$ 算出 $m$，就能直接写出 $l_3$ 的方程为 $2x + 3y + 5= 0$．

直线关于直线对称 情况 2：目标直线和对称轴相交 标准做法

求 $l_1$：$Ax + By + C = 0$ 关于 $l_2$：$Dx + Ey + F = 0$ 的对称直线 $l_3$ 的方程．这里保证 $l_1 \nparallel l_2$．

计算量最小的标准做法如下：

考虑到 $l_1$ 和 $l_2$ 的交点必在 $l_3$ 上，求出 $l_1$ 和 $l_2$ 的交点，它在 $l_3$ 上．

然后我们再求出 $l_1$ 上任意一个不同于 $l_1$ 和 $l_2$ 交点的点，求它关于 $l_2$ 的对称点，它也在 $l_3$ 上．

确定 $l_3$ 上的两个点后我们就能确定它的方程了．

例题 2.6.2

求直线 $l_1$：$x + y - 1 = 0$ 关于直线 $l_2$：$3x - y - 3 = 0$ 对称的直线 $l_3$ 的方程．

例题 2.6.2

易求得 $l_1$ 和 $l_2$ 的交点为 $(1, 0)$，该点也在 $l_3$ 上．

考虑 $l_1$ 上任意一个不同于 $(1, 0)$ 的点 $(0, 1)$，求出它关于 $l_2$ 的对称点（求解过程省略），为 $(\df{12}5, \df 1 5)$．

$l_3$ 过 $(1, 0)$ 和 $(\df{12}5, \df 1 5)$，计算得斜率为 $\df{1}7$，则 $l_2$ 的方程为 $y = \df{1}7(x - 1)$，即 $x - 7y - 1 = 0$．

直线关于直线对称 选填速算技巧

求 $l_1$：$ax + by + c = 0$ 关于 $l_2$：$Ax + By + C = 0$ 的对称直线 $l_3$ 的方程．这里保证 $l_1 \nparallel l_2$．

任意曲线关于直线对称后的方程

设任意曲线 $\Gamma$ 的方程为 $F(x, y) = 0$，则其关于 $Ax + By + C = 0$ 对称的曲线 $\Gamma'$ 方程为

$$F(x - 2tA, y - 2tB) = 0$$

其中 $t = \df{Ax + By + C}{A^2 + B^2}$．

原因：点 $P(x_0, y_0)$ 在 $\Gamma'$ 上，等价于其关于 $Ax + By + C = 0$ 的对称点 $(x_0 - 2tA, y_0 - 2tB)$ 在 $\Gamma$ 上．

现在考虑 $\Gamma$ 为直线 $ax + by + c = 0$ 的情形，我们有其对称后的直线为 $a(x - 2tA) + b(y - 2tB) + c = 0$．整理方程：

$$\begin{aligned} a(x - 2tA) + b(y - 2tB) + c &= 0\\ ax - 2Aat + by - 2Bbt + c &= 0 \\ ax + by + c &= (2Aa + 2Bb)t \\ ax + by + c &= (2Aa + 2Bb) \times \df{Ax + By + C}{A^2 + B^2}\\ \df{ax + by + c}{Ax +By + C} &= \df{2Aa + 2Bb}{A^2 + B^2} \end{aligned}$$

因此，遇到 $ax + by + c = 0$ 对 $Ax +By + C = 0$ 对称，可以直接写下结果直线的方程

$$\df{ax + by + c}{Ax +By + C} = \df{2Aa + 2Bb}{A^2 + B^2}$$

然后化简即可．

注意区分：小写字母 $a$，$b$，$c$ 代表被对称的直线上的系数；大写 $A$，$B$，$C$ 代表对称轴上的系数．

辅助记忆技巧

等号左侧：

$$\df {ax + by + c}{Ax + By + C}$$

将 分数线 视作平面镜，一般来说光线在平面镜的上方，所以平面镜上方刻画的是 光线（即 被对称的线）的信息，平面镜下方刻画的是 平面镜（即 对称轴）的信息．

等号右侧：

$$\df{2Aa + 2Bb}{A^2 + B^2}$$

可以视作光线经过反射了，平面镜下方仍然只与平面镜的信息有关（$A^2 + B^2$），平面镜上方为反射光线的信息，均匀混合了入射光线和平面镜的信息，变为 $2Aa + 2Bb$．

注意上面的技巧只是辅助记忆，没有任何实际意义．

例题 2.6.2

求直线 $l_1$：$x + y - 1 = 0$ 关于直线 $l_2$：$3x - y - 3 = 0$ 对称的直线 $l_3$ 的方程．

例题 2.6.2 解答（技巧）

直接列出 $l_3$ 的方程为 $\df{x + y - 1}{3x - y - 3} = \df{2 \times 1 \times 3 + 2 \times 1 \times (-1)}{3^2 + (-1)^2} = \df{2}5$，化简得 $x - 7y - 1 = 0$．

上面这个速算技巧并没有用到 $l_1$ 和 $l_2$ 必须相交，但是 $l_1 \parallel l_2$ 的情形计算对称直线本来就相当简单，采用这个速算反而更麻烦．所以我们在 $l_1 \nparallel l_2$ 的选填中才考虑使用此技巧．

光线反射问题

考虑这样一个模型：

已知从点 $A$ 发出一条激光，经过一条直线 $l$ 的反射，反射光线在点 $B$ 处被吸收．

现求解入射点 $C$ 的坐标，以及光线从 $A$ 到 $B$ 走过的路径长度．

最简单的操作步骤是：

• 将 $A$ 沿 $l$ 对称到 $A'$．
• 连接 $A'B$．
• $A'B$ 与 $l$ 的交点即入射点 $C$，光线走过的路程即 $\lv A'B \rv$．

不难根据平面几何知识证明这么做的正确性，限于篇幅这里不给出证明．

例题 2.7.1

一光线从点 $A(-3, 5)$ 出发射到直线 $3x - 4y + 4 = 0$ 上，反射后经点 $B(2, 15)$，求光线从 $A$ 点反射到 $B$ 点经过的路程．

例题 2.7.1 解答

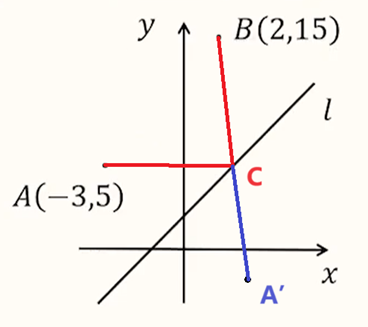
将 $(-3, 5)$ 关于 $3x - 4y + 4 = 0$ 对称，用速算技巧，算出 $t = \df{3 \times (-3) - 4 \times 5 +4}{3^2 + (-4)^2} = -1$，$A'$ 坐标为 $(-3, 5) - 2t(3, -4) = (3, -3)$．随后不难算出 $|A'B| = 5\sqrt{13}$，即为答案．

例题 2.7.2

已知 $A(3, 0)$，$B(0, 3)$，从 $P(1, 0)$ 射出的光线经直线 $AB$ 和直线 $OB$ 先后两次反射后回到点 $P$，求光线经过的路程．

例题 2.7.2 解答

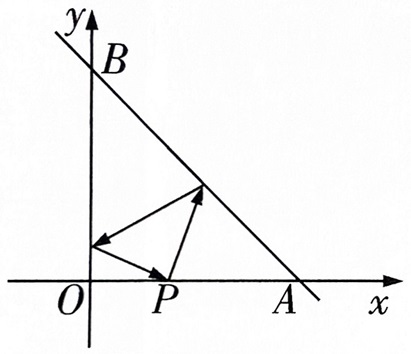
作出 $P$ 关于 $AB$ 的对称点 $P_1$ 和关于 $BO$ 的对称点 $P_2$，$|P_1P_2|$ 即为答案．

这里两个对称都是特殊情形（一个坐标轴，一个斜率 $\pm 1$），所以对称点坐标都很好求．因此过程不再赘述，$P_1(3, 2)$，$P_2(-1, 0)$，答案为 $2\sqrt 5$．

例题 2.7.3

一束光从 $P(1, 2)$ 出发，经 $x$ 轴反射后，射到线段 $y = -x + b,\ x \in [3, 5]$ 上的点 $M$．

• （1）若 $b = 8$，求反射光线斜率的取值范围．
• （2）若 $b \ge 6$，设光走过的路径长度的最小值为 $S(b)$，求 $S(b)$ 的解析式．

例题 2.7.3 解答

光从 $P(1, 2)$ 经 $x$ 轴反射射到线段上，可以看作光从 $P'(1, -2)$ 穿过 $x$ 轴射向线段．

（1）

等价于过 $(1, -2)$ 的直线过线段 $y = -x + 8, \ x \in [3, 5]$．

裸的过定点直线交于线段求斜率范围问题，过程不再赘述，答案为 $[\df 5 4, \df 7 2]$．

（2）

我们先解决一个子问题：

例题 2.7.3 子问题

已知一点 $P$ 和一线段 $AB$，求 $P$ 和线段 $AB$ 上某一点的距离最小值．

例题 2.7.3 子问题解答

作 $PH \perp AB$，显然，如果 $H$ 在线段 $AB$ 上，则 $|PH|$ 就是所求最小值．

如果 $H$ 落在线段 $AB$ 外，则 $PH$ 取不到：

• 如果 $H$ 落在 $A$ 的远离线段 $AB$ 方向的一侧，则距离最小值取在 $|PA|$．
• 如果 $H$ 落在 $B$ 的远离线段 $AB$ 方向的一侧，则距离最小值取在 $|PB|$．

令 $A(3, b - 3)$，$B(5, b - 5)$，现在所求就是 $P'$ 到线段 $AB$ 上某一点的距离最小值．

从 $P'$ 到直线 $AB$ 作垂，$AB$ 斜率 $\pm1$，垂足可以速算．$P'(1, -2)$ 关于 $y = b - x$ 的对称点为 $P''(b + 2, b - 1)$，垂足 $H$ 为 $P'P''$ 的中点 $(\df{b + 3}2, \df{b - 3}2)$．

• 当 $b \in [6, 7]$ 时，$\df{b + 3}2 \in [3, 5]$，$H$ 在线段 $AB$ 上．距离最小值为 $P'H = \df{\sqrt 2(b + 1)}2$．
• 当 $b \in (7, +\infty)$ 时，$\df{b + 3}2 \in (5, +\infty)$，$H$ 在 $B$ 的偏离线段 $AB$ 的一侧，则距离最小值为 $P'B = \sqrt{b^2 - 6b + 25}$．

综上，最短路程 $S(b) = \begin{cases}\df{\sqrt 2(b + 1)}2 & b \in [6, 7] \\[1em] \sqrt{b^2 - 6b + 25} & b \in (7, +\infty)\end{cases}$．

三角形高线所在直线

对于任意一个三角形 $\triangle PQR$，$QR$ 边上的高线所在直线，等价于一条同时满足下面两个条件的直线：

• 该直线与直线 $QR$ 垂直．
• $P$ 在该直线上．

这就是刻画三角形高线所在直线的方法．

例题 2.8

已知 $\triangle ABC$ 中，$AC$、$AB$ 边上的高所在直线分别为 $2x - 3y + 1 = 0$ 和 $x + y = 0$，顶点 $A(1, 2)$，求 $BC$ 所在直线的方程．

解决三角形问题，第一步是画图辅助理解．请读者不要画坐标系 1:1 还原，为了足够的效率，直接随手画一个三角形，并合理地表示对应的高线、中线和角平分线，就已经足够做题了．下面是一个推荐的画图示例：

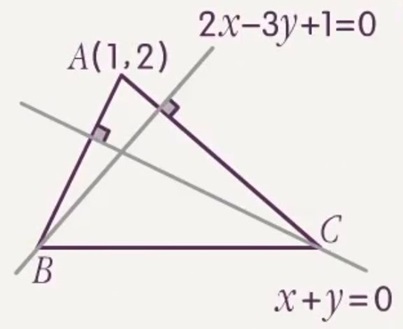
题目中的一条高线所在直线可以等价为该直线的两条信息，共可给出四条信息：

• $AC$ 的法向量和 $AC$ 边的高线所在直线的法向量垂直，即 $AC$ 法向量为 $(3, 2)$．
• $B$ 在 $AC$ 边的高线所在直线上．
• $AB$ 的法向量和 $AB$ 边的高线所在直线的法向量垂直，即 $AB$ 法向量为 $(1, -1)$．
• $C$ 在 $AB$ 边的高线所在直线上．

例题 2.8 解答

$AC$ 与 $2x - 3y + 1 = 0$ 垂直，则其所在直线法向量为 $(3, 2)$，不妨设

$$AC \colon 3x + 2y + C = 0$$

其过点 $A$，可知 $3 \times 1 + 2 \times 2 + C = 0$，解得 $C = -7$，即 $AC$ 所在直线方程为 $3x + 2y - 7 = 0$．

同理，可知 $AB$ 所在直线方程为 $x - y + 1 = 0$．

联立 $x - y + 1 = 0$ 和 $2x - 3y + 1 = 0$ 可知 $B(-2, -1)$．

联立 $3x + 2y - 7 = 0$ 和 $x + y = 0$ 可知 $C(7, -7)$．

已知两点，可知 $BC$ 解析式为 $2x + 3y + 7 = 0$．

三角形中线所在直线

刻画中线所在直线的方法：中线 同时经过顶点和对边中点．

例题 2.9

已知 $\triangle ABC$ 中，$AC$、$AB$ 边上的中线所在直线分别为 $3x - 2y + 2 = 0$ 和 $3x + 5y - 12 = 0$，顶点 $A(-4, 2)$，求 $BC$ 所在直线的方程．

画出示意图，还是一样，不用画出坐标系，随便画三角形足够分析．

例题 2.9 解答

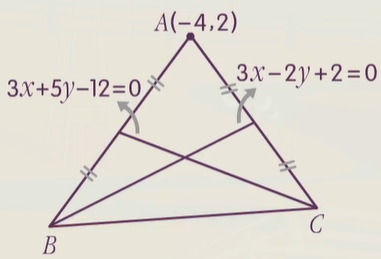
设 $B(x_B, y_B)$，$C(x_C, y_C)$．

$AC$ 中线经过点 $B$ 和 $AC$ 的中点：

$$\begin{cases}3x_B - 2y_B + 2 = 0 \\[1em] 3(\df{x_C - 4}2) - 2(\df{y_C + 2}2) + 2 = 0\end{cases}$$

$AB$ 中线经过点 $C$ 和 $AB$ 的中点：

$$\begin{cases}3x_C + 5y_C - 12 = 0 \\[1em] 3(\df{x_B - 4}2) + 5(\df{y_B + 2}2) - 12 = 0\end{cases}$$

四个未知数，四个方程，可解（而且可以拆成两个二元一次方程组）．

解得 $B(2, 4)$，$C(4, 0)$，可得出 $BC$ 的方程为 $2x + y - 8 = 0$．

角平分线所在直线

三角形的角平分线所在直线与高线、中线不太一样：它只与三角形的两条边有关，而与第三条边无关．角平分线所在直线只是两个边的角平分线而已，不必局限于三角形的讨论范围．所以这里直接讨论更一般的角平分线处理策略．

对于 $\angle BAC$，其角平分线所在直线 $l$ 等价于这样一条直线：$AB$ 和 $AC$ 关于该直线对称．

根据对称的知识可以进一步刻画条件为：直线 $AB$ 上一个不是点 $A$ 的点，关于 $l$ 对称后在直线 $AC$ 上．

用「对称」刻画这个条件，是比通过 夹角公式暴力地表述出两个夹角相等 要简单的．

例题 2.10

已知 $A(3, 1)$，$B(-1, 2)$，若 $\angle ACB$ 的平分线在直线 $y = x + 1$ 上，求直线 $AC$ 的方程．

例题 2.10 解答

$\angle ACB$ 的平分线在直线 $y = x + 1$ 上，等价于 $B$ 关于 $y = x + 1$ 的对称点 $B'$ 在直线 $AC$ 上．对称直线还是斜率为 $\pm 1$ 的特殊直线，所以 $B'$ 坐标可以用技巧计算．我们有 $B'(1, 0)$．

观察到所求的直线 $AC$ 方程其实就是直线 $AB'$ 的方程，两点坐标已知，方程可解．答案为 $x - 2y - 1 = 0$．

面积

知道任意三角形的三个点坐标，就可以知道：

• 三角形的 三边长（两点距离公式）．
• 三角形的 三边直线方程（两点确定直线）．
• 三角形的 三高（点到直线距离公式）．

直接选取一组底和高计算面积即可．从此远离割补法．

另外，平行四边形的面积为底乘高：

• 底使用两点距离公式计算．
• 高可以使用 平行线间距离公式 计算．

例题 2.11.1

已知直线 $l_1$ 过定点 $M(6, 4)$，且与直线 $l_2$：$y = 4x$ 交于第一象限的点 $A$，与 $x$ 轴正半轴交于点 $B$，求使得 $\triangle OAB$（$O$ 为坐标原点）面积最小时的直线 $l_1$ 的方程．

例题 2.11.1 解答

当 $l_1$ 不存在斜率时，$l_1$：$x = 6$，$A(6, 24)$，$B(6, 0)$，$\triangle OAB$ 面积为 $72$．

当 $l_1$ 斜率为 $k$ 时，由于 $l_1$ 与 $y = 4x$ 相交且与 $x$ 轴相交，有 $k \ne 0$ 且 $k \ne 4$．

此时 $l_1$：$y - 4 = k(x - 6)$，可解得 $A(\df{4 - 6k}{4 - k}, \df{16 - 24k}{4 - k})$，$B(\df{6k - 4}{k}, 0)$．

$A$ 位于第一象限，$B$ 位于正半轴，则 $\df{4 - 6k}{4 - k} > 0$ 且 $\df{6k - 4}k > 0$，解得 $k < 0$ 或 $k > 4$．

面积可表示为函数 $\df 1 2 \cdot \df{6k - 4}{k} \cdot \df{16 - 24k}{4 - k}$，化简得

$$S(k) = \df{72k^2 - 96k + 32}{k^2 - 4k}, \quad k \in (-\infty, 0) \cup (4, +\infty)$$

现在要求这个 二次比二次型函数 的最小值，这一部分是 函数 那一章的基础内容．

分离常数得 $72 + 32 \cdot \df{1}{\fr{k^2 - 4k}{6k + 1}}$，分析分母 $f(k) = \df{k^2 - 4k}{6k + 1}$：

• 如果 $f(k)$ 能取到负数，$S(k)$ 最小值在 $f(k)$ 取到 负数中的最大值 时取到．
• 如果 $f(k)$ 取不到负数，$S(k)$ 最小值在 $f(k)$ 取到 最大值 时取到．

设 $t = 6k + 1$，则 $t \in (-\infty, 1) \cup (25, +\infty)$．于是

$$f(k) = \df{k^2 - 4k}{6k + 1} = \df{t^2 - 26t + 25}{36t} = \df{1}{36}(t + \df{25}t - 26)$$

对勾函数的性质给出

$$t + \df {25} t \in (-\infty, -10) \cup (26, +\infty)$$

不难看出 $f(k)$ 可取负数，且能取到的负数最大值为 $\df 1 {36}(-10 - 26) = -1$，此时 $t = -5$，$k = -1$．

因此面积取到最小值时，$l_1$ 斜率为 $-1$．根据点斜式有 $y - 4 = -(x - 6)$，整理得 $x + y = 10 = 0$．

下面提供一个计算量小于上面做法的另一种做法．

例题 2.11.1 解答 2

我们可以换种方式对所有条件作如下等价变换：$A$ 是一个自由在 $l_2$ 第一象限上移动的动点，$B$ 是一个在 $x$ 轴正半轴的动点．始终有 $A$，$M$，$B$ 始终三点共线．求面积最小值．

设 $A(a, 4a)$，其中 $a > 0$；$B(b, 0)$，其中 $b > 0$．则 $A$，$M$，$B$ 三点共线．可以刻画为直线 $MA$ 和直线 $MB$ 的方向相同．一般选择采用斜率刻画（斜率相等或同时不存在）．

当直线 $MA$ 和直线 $MB$ 斜率均不存在，即 $l_1$：$x = 6$ 时，显然面积 $S = 72$．

当它们斜率存在且相同时，$k_{MA} = k_{MB}$，即 $\df{4a - 4}{a - 6} = \df{4}{6 - b}$．不难解出 $b = \df{5a}{a - 1}$．

$b > 0$，所以有 $\df{5a}{a - 1} > 0$，综合 $a > 0$，有 $a > 1$．

面积 $S = \df 1 2 \cdot \df{5a}{a - 1} \cdot 4a = \df{10a^2}{a - 1} = 10(a - 1 + \df1{a - 1} + 2) \ge 40$，当且仅当 $a - 1 = \df{1}{a - 1}$ 时等号成立，此时 $a = 2$，$A(2, 8)$（注意这里基本不等式用到了 $a - 1 > 0$ 这一条件）．

$A(2, 8)$，$M(6, 4)$，不难解得 $l_1$ 方程为 $x + y - 10 = 0$．

为什么解法 2 比解法 1 的计算量明显少了很多？下面列举两个原因．

原因一：

三角形的面积是 $A$ 的纵坐标与 $B$ 的横坐标的积的一半．想要计算面积的最小值，$A$ 的纵坐标和 $B$ 的横坐标形式应比较简单．

• 解法 1 采用的思路是：设出 $l_1$ 的斜率 $k$，用 $k$ 表达两个点的坐标．
• 解法 2 采用的思路是：直接用参数表达一个坐标，再用共线条件表达另一个坐标．

不难发现，后者得到的坐标形式明显简单许多——因为后者有一个坐标已经是单纯的字母 $a$ 了，前者中两个坐标都是含 $k$ 的一次分式，乘一下就变二次比二次了．

原因二：

考虑题目给出的两个制约条件：$A$ 在 $y = kx$ 的 第一象限，$B$ 在 $x$ 轴的 正半轴．

• 解法 1 对这两个条件的制约是对 两个含 $k$ 的一次分式的范围制约．
• 解法 2 对这两个条件的制约直接被表达为简单的 $a > 0$ 和 $\df{5a}{a - 1} > 0$．

可以发现后者更为简单．

无论是原因一——所求内容的表达复杂度，以及原因二——制约条件的表达复杂度，后者的复杂度都更低．因此，做题时，可注意题目中的条件是否能等价为另一种形式，从而让计算复杂度更低．

例题 2.11.2

四边形 $OABC$ 的四个顶点坐标分别为 $O(0, 0)$，$A(6, 2)$，$B(4, 6)$，$C(2, 6)$，直线 $y = kx$（$\df 1 3 < k < 3$）把四边形 $OABC$ 分成两部分，设 $S(k)$ 表示靠近 $x$ 轴部分的面积，求 $S(k)$ 的解析式．

本题比较裸，只提供答案，供读者参考．

例题 2.11.2 解答

$$S(k) = \begin{cases} \df{42k - 14}{k + 2}, & k \in (\df 1 3, \df 3 2 ) \\[1em] 26 - \df{18}k, & k \in [\df 3 2, 3 ) \end{cases}$$