等差数列

等差数列基础

等差数列基本概念

如果一个数列从第二项起，每一项与前一项的差都为一个常数 $d$（difference），则将这个数列称作 等差数列，$d$ 称作该数列的 公差．

即对于等差数列 $\{a_n\}$，其差分 $\{D_n\}$ 满足

$$D_n = \begin{cases} a_1, & n = 1 \\ d, & n \ge 2 \end{cases}$$

对 $\{D_n\}$ 做前缀和可得

$$a_n = a_1 + (n - 1)d$$

该式为 等差数列的通项公式．很明显，确定 $a_1$ 和 $d$ 后，等差数列确定，而只确定其中之一则无法确定等差数列．

通项公式变形：

$$n = \df{a_n - a_1}{d} + 1$$

可以用来算 某一项是一个已知等差数列的第几项，甚至不局限于纯等差数列：

例题 1.1

$2^3, 2^7, 2^{11}, \ldots, 2^{103}$ 共有多少项？

例题 1.1 解答

这虽然是一个等比数列，但是看指数就能知道总共有几项，而指数是等差数列．

项数为 $\df{103 - 3}{4} + 1 = 26$．

等比数列求和公式需要代入项数，所以看到 $2^3 + 2^7 + 2^{11} + \cdots + 2^{103}$，虽然我们暂时还没学习等比数列求和公式，也应 立刻明确其项数的计算公式，从而正确的算出它的项数，这是后面做等比数列求和的 非常重要 的基础．

同理，等差数列求和公式也要知道项数，如 $52 + 54 + 56 + \cdots + 660$ 的项数是 $\df{660 - 52}{2} + 1 = 305$．

总之，算等差数列的项数 是一项 非常基本的求和基础技能，后面将不再强调．

对于长度为 $3$ 的等差数列 $a, b, c$，称 $b$ 是 $a$ 和 $c$ 的 等差中项．

由 $b - a = c - b$ 可以推出，等差中项等价于 算术平均值，即

$$b = \df{a + c}2 \iff 2b = a + c$$

等差数列的英文是 Arithmetic Progression，简称 AP．Arithmetic 意为「算术的」，正与这里的「算术平均值」对应．

有限长度等差数列

这一节讲一个条件处理策略：如果题目给定条件「$a_1, a_2, \ldots, a_k$ 为等差数列」，我们可以将它 等价 地转化为：

$$\begin{aligned} a_1 + a_3 &= 2a_2 \\ a_2 + a_4 &= 2a_3 \\ & \cdots \\ a_{k - 2} + a_k &= 2a_{k - 1} \end{aligned}$$

共 $k - 2$ 个等式．

也即，题目但凡涉及到 有限个数 构成 有限长度的等差数列，设长度为 $k$，转成 $k - 2$ 个等式在绝大多数情况下是最简单的．

例题 1.2

已知 $a$，$b$，$c$ 成等差数列，证明 $a^2 - bc$，$b^2 - ac$，$c^2 - ab$ 成等差数列．

例题 1.2 解答

条件等价于 $a + c = 2b$．

结论等价于 $a^2 - bc + c^2 - ab = 2(b^2 - ac)$．现在开始证明．

证明等式成立，可以将左侧减去右侧然后证明结果为 $0$．

$$\begin{aligned} & \phantom{=} (a^2 - bc) + (c^2 - ab) - 2(b^2 - ac) \\ & = a^2 + c^2 - 2b^2 - bc - ab + 2ac \\ & = (a + c)^2 - b(a + c) - 2b^2 \\ & = (2b)^2 - 2b^2 - 2b^2 \\ & = 0 \end{aligned}$$

等差数列前缀和

设等差数列 $\{a_n\}$ 的前缀和为 $\{S_n\}$，求 $S_n$．

我们有

$$2S_n = (a_1 + a_n) + (a_2 + a_{n - 1}) + \cdots + (a_{n - 1} + a_2) + (a_n + a_1)$$

且对于任意 $1 \le i \le n$，有

$$a_i + a_{n - i} = a_1 + (i - 1)d + a_1 + (n - i)d = 2a_1 + (n - 1)d = a_1 + a_n$$

因此上面的所有括号内的结果可以统一为 $a_1 + a_n$，有

$$2S_n = n(a_1 + a_n)$$

于是

$$S_n = \df{n(a_1 + a_n)}2$$

将 $a_n$ 展开，可得

$$S_n = \red{n}a_1 + \df{n(n \red{-} 1)}2 d$$

$a_1$ 与 $d$ 求 $\{S_n\}$ 通项公式的基本公式，两个红色部分为易错点，着重记忆．

等差数列的性质

下设 $\{a_n\}$ 为等差数列．

等差数列性质一

$$a_n - a_m = (n - m)d$$

该性质可以直接由通项公式展开推出．上面的变形式

$$a_n = a_m + (n - m)d$$

可以用来 已知等差数列的任意一项与公差，求任一另外项．

另外一个变形

$$d = \df{a_n - a_m}{n - m}$$

可以用来 已知任意两项求公差．

等差数列性质二（下标守恒定律）

定义等差数列的若干项相加、相减（可以带系数，不能带次数）形成的式子为「等差加减式」，如

$$a_3 + a_4 + a_5$$ $$2a_9 - a_{10}$$ $$a_5 - a_6 + a_7 - a_8 + a_9$$

对于「等差加减式」，我们定义两个属性：

• 系数和：即所有 $\{a_n\}$ 的 系数 之和．上面三个式子的系数和分别为 $3$，$1$，$1$．
• 下标和：即所有 $\{a_n\}$ 的 下标与系数的积 之和．上面三个式子的下标和为 $12$，$8$，$7$．

结论：对于两个「等差加减式」，如果它们的系数和与下标和均分别相同，则结果一定相同．笔者将这个结论称作 下标守恒定律．

比如我们有

$$a_3 + a_4 + a_5 = 3a_4$$

两边系数和均为 $3$，下标和均为 $12$．

$$2a_9 - a_{10} = a_8$$

两边系数和均为 $1$，下标和均为 $8$．

$$a_5 - a_6 + a_7 - a_8 + a_9 = a_7$$

两边系数和均为 $1$，下标和均为 $7$．

下标守恒定律的误用

$$a_7 = a_3 + a_4$$

错因

下标守恒定律除了 下标和相同 外，还必须保证两边 系数和相同．

上面的式子左边系数和为 $1$，右边系数和为 $2$，因此不一定成立．

证明：

$$\begin{aligned} & \phantom = c_1a_{x_1} + c_2a_{x_2} + \cdots + c_ka_{x_k} \\ & = c_1(a_1 + (x_1 - 1)d) + c_2(a_1 + (x_2 - 1)d) + \cdots + c_k(a_1 + (x_k - 1)d) \\ & = (c_1 + c_2 + \cdots + c_k)a_1 + (c_1x_1 + c_2x_2 + \cdots + c_kx_k - (c_1 + c_2 + \cdots + c_k))d \end{aligned}$$

系数和 $c_1 + c_2 + \cdots + c_k$ 与下标和 $c_1x_1 + c_2x_2 + \cdots + c_kx_k$ 确定时，结果确定．

下标守恒定律的推论：同一个等差数列的两个「等差加减式」，如果它们的 系数和之比 等于 下标和之比 等于 $k$，则它们的 结果之比 也为 $k$．

例题 1.4

等差数列 $\{a_n\}$，已知 $a_3 + a_4 + a_5 + a_6 + a_7 = 25$，求 $a_2 + a_8$ 的值．

例题 1.4 解答

两个「等差加减式」的系数和之比为 $5:2$，下标和之比为 $25:10 = 5:2$．

因此结果之比也为 $5:2$，答案为 $10$．

下标守恒定律用来避开 $a_1$ 与 $d$，直接沟通数列 $\{a_n\}$ 多个项之间的关系．

等差数列性质三

等差数列 $\{a_n\}$，对任意正整数 $k$，我们写出数列

$$a_1 + a_2 + \cdots + a_k, a_{k + 1} + a_{k + 2} + \cdots + a_{2k}, a_{2k + 1} + a_{2k + 2} + \cdots + a_{3k}, \ldots$$

注意到 $a_{i + k} - a_i = kd$，因此上面这个数列是一个公差为 $k^2d$ 的 等差数列．

根据区间和为两个前缀和的差，我们还可以写成

$$S_k, S_{2k} - S_k, S_{3k} - S_{2k}, \ldots$$

为公差为 $k^2d$ 的 等差数列．

这个性质也是在说 $S_k, S_{2k}, S_{3k}, \ldots$ 是一个 二阶等差数列（其差分是一个等差数列）．

该性质通常适合 题目中没有出现 $\{a_n\}$，而出现了若干下标均为某个正整数 $k$ 的倍数的 $\{S_n\}$ 时使用．

等差数列性质四

$n$ 为奇数时，根据下标守恒定律有

$$a_1 + a_n = 2a_{\frac{n + 1} 2}$$

此时根据

$$S_n = \df{n(a_1 + a_n)}2$$

有

$$S_n = na_{\frac {n + 1} 2}$$

逆公式：

$$a_n = \df 1 n S_{2n - 1}$$

逆公式中的 $n$ 可以是任意整数，而导出的 $\{S_n\}$ 的下标一定是奇数．

等差数列性质五

$\{\df{S_n}n\}$ 是一个首项为 $a_1$，公差为 $\* \df 1 2 d$（$d$ 为 $\{a_n\}$ 的公差）的 等差数列．反过来，$\{\df{S_n}n\}$ 是等差数列也可推出 $\{a_n\}$ 是等差数列．

后面会了解到等差数列的函数形式 $S(n) = An^2 + Bn$，学到那里再回看这条性质就明白了．

等差数列题型

等差数列信息求解（基本量法）

基本量法：通过将未知量转为 $a_1$ 和 $d$ 的式子，将条件转为若干 $a_1$ 和 $d$ 构成的二元方程组，然后解方程组．

例题 2.1.1

等差数列 $\{a_n\}$，已知 $a_6 = 9$，$a_3 = 3a_2$，求 $a_1$ 的值．

考虑将所有的 $a_n$ 等价转化为 $a_1 + (n - 1)d$．

例题 2.1.1 解答

$$\begin{cases} a_1 + 5d = 9 \\ a_1 + 2d = 3(a_1 + d) \end{cases} \iff \begin{cases} a_1 = -1 \\ d = 2 \end{cases}$$

例题 2.1.2

设 $\{a_n\}$ 为等差数列，$S_n$ 为前 $n$ 项和，若 $S_6 = 8S_3$，$a_3 - a_5 = 8$，求 $a_{20}$ 的值．

全部转化为 $a_1$ 和 $d$ 暴力计算即可．

例题 2.1.2 解答

$$\begin{cases} 6a_1 + 15d = 8(3a_1 + 3d) \\ -2d = 8 \end{cases} \iff \begin{cases} a_1 = 2 \\ d = -4 \end{cases} \implies a_{20} = -74$$

这里 $a_3 - a_5 = -2d$ 小用了一下等差数列性质一．

如果只给出了一个条件，无法构成方程组，不能求出 $a_1$ 与 $d$ 的具体值，只能得到它们的关系式，可以考虑 消元．

例题 2.1.3

已知等差数列 $\{a_n\}$，$a_1 \ne 0$，$a_2 = 3a_1$，求 $\df{S_{10}}{S_5}$．

例题 2.1.3 解答

$$a_2 = 3a_1 \iff a_1 + d = 3a_1 \iff d = 2a_1$$$$\df{S_{10}}{S_5} = \df{10a_1 + 45d}{5a_1 + 10d} = \df{10a_1 + 90a_1}{5a_1 + 20a_1} = 4$$

等差数列信息求解（简化计算）

有时也要善用等差数列的性质（尤其是下标守恒定律），等价转化条件．

例题 2.2.1

等差数列 $\{a_n\}$，已知 $a_2 + a_5 + a_8 + a_{11} = 48$，求 $a_6 + a_7$ 的值．

例题 2.2.1 解答

「等差加减式」，系数和之比与下标和之比均为 $2 : 1$，结果之比也为 $2:1$，答案为 $24$．

例题 2.2.2

在等差数列 $\{a_n\}$ 中，$a_9 = \df 1 2 a_{12} + 3$，求 $S_{11}$．

例题 2.2.2 解答

所求 $S_{11} = 11a_6$，只需求 $a_6$．

根据下标守恒定律，有

$$a_9 - \df 1 2 a_{12} = \df 1 2 a_6$$

因此 $a_6 = 6$，$S_{11} = 66$．

例题 2.2.3

已知两个等差数列 $\{a_n\}$，$\{b_n\}$，前缀和分别为 $\{S_n\}$，$\{T_n\}$，已知 $\df{S_n}{T_n} = \df{7n + 2}{n + 3}$，求 $\df{a_7}{b_7}$ 的值．

例题 2.2.3 解答

$$\df{a_7}{b_7} = \df{13a_7}{13b_7} = \df{S_{13}}{T_{13}} = \df{93}{16}$$

例题 2.2.4

设 $\{S_n\}$ 是等差数列 $\{a_n\}$ 的前缀和，若 $\df{S_3}{S_6} = \df 1 3$，求 $\df{S_6}{S_{12}}$ 的值．

例题 2.2.4 解答

遇到这种 $\{S_n\}$ 的下标都是某个正整数的几倍 的，可以考虑使用等差数列性质四．

我们先写出这个等差数列：

$$S_3, S_6 - S_3, S_9 - S_6, S_{12} - S_9$$

设 $S_3 = a$，则 $S_6 = 3a$，$S_6 - S_3 = 2a$．上数列为等差数列，因此 $S_9 - S_6 = 3a$，$S_{12} - S_9 = 4a$．

进一步可知 $S_9 = 6a, S_{12} = 10a$．因此 $\df{S_6}{S_{12}} = \df{3a}{10a} = \df 3 {10}$．

等差数列的判定

作差成常数判定等差数列

只需证明 $a_{n + 1} - a_n$ 对任意 $n \in \N^\ast$ 为常数即可．证明 $a_n - a_{n - 1}$ 对任意 $n \ge 2, \quad n \in \N^\ast$ 成立也可，看条件给出的是 $a_n$ 与 $a_{n + 1}$ 的关系还是 $a_n$ 与 $a_{n - 1}$ 的关系，灵活选择．

例题 2.3.1

已知数列 $\{a_n\}$ 满足 $a_1 = 4$，$a_{n + 1} = \df{a_n}{a_n + 1}$，求证：$\{\df 1 {a_n} \}$ 是等差数列．

例题 2.3.1 解答

只需证

$$\df 1 {a_{n + 1}} - \df 1 {a_n} = \text{const.}, \quad n \in \N^\ast$$

而

$$\df 1 {a_{n + 1}} - \df 1 {a_n} = \df{a_n + 1}{a_n} - \df 1 {a_n} = \df{a_n}{a_n} = 1$$

证毕．

例题 2.3.2

已知数列 $\{a_n\}$ 满足 $a_1 = 1$，$n(a_{n + 1} - a_n) = a_n + n^2 + n, \quad n \in \N^\ast$，求证：$\{\df {a_n} n \}$ 是等差数列．

例题 2.3.2 解答

只需证

$$\df{a_{n + 1}}{n + 1} - \df {a_n} n = \text{const.}, \quad n \in \N^\ast$$

对条件变形：

$$\begin{aligned} n(a_{n + 1} - a_n) &= a_n + n^2 + n \\ na_{n + 1} &= (n + 1)a_n + n(n + 1) \\[1ex] \df{a_{n + 1}}{n + 1} &= \df{a_n}n + 1 \\[1em] \df{a_{n + 1}}{n + 1} - \df{a_n}n &= 1 \end{aligned}$$

证毕．

等差中项判定等差数列

还可以通过证明 $a_n + a_{n + 2} = 2a_{n + 1}$ 对任意 $n \in \N^\ast$ 成立证明等差数列，两者是等价的．可以在大题中直接使用．

当然换个写法，$a_{n - 1} + a_{n + 1} = 2a_n$ 对任意 $n \in \N^\ast, n \ge 2$ 成立也一样．

例题 2.3.3

已知正项数列 $\{a_n\}$ 满足 $2{a_n}^2 = {a_{n - 1}}^2 + {a_{n + 1}}^2$ 对任意 $n \in \N^\ast, n \ge 2$ 成立，$a_1 = 1$，$a_2 = 2$，求 $a_{34}$ 的值．

例题 2.3.3 解答

题目给出的条件和等差中项十分类似，但每一项都多了个平方．对于这种数列每一项 算术结构相同 的式子，可以考虑构造新数列．

令 $b_n = {a_n}^2$，则有 $2b_n = b_{n - 1} + b_{n + 1}$，因此 $\{b_n\}$ 是等差数列．

而 $b_1 = {a_1}^2 = 1$，$b_2 = {a_2}^2 = 4$，可知 $b$ 首项为 $1$，公差为 $b_2 - b_1 = 3$．

$b_n = 1 + 3(n - 1) = 3n - 2$．由于 $\{a_n\}$ 为正项数列，因此 $a_{34} = \sqrt{b_{34}} = \sqrt{100} = 10$．

等差数列前缀和最值

等差数列 $\{a_n\}$，前缀和 $\{S_n\}$：

• $d = 0$：$\{a_n\}$ 为 常数列．任意一项同时为最大项与最小项．
• $a_1 \le 0$，$d < 0$：$\{a_n\}$ 首项非正，其余恒负，$\{S_n\}$ 无 最小项，唯一最大项 为 $S_1$．
• $a_1 \ge 0$，$d > 0$：$\{a_n\}$ 首项非负，其余恒正，$\{S_n\}$ 无 最大项，唯一最小项 为 $S_1$．

上面三种情况都是很平凡的，不常考，考到了也是简单题，直接做即可．

下面两种情况则比较常考，需要着重注意：

• $a_1 < 0$，$d > 0$：$\{a_n\}$ 先负后正，$\{S_n\}$ 无 最大项，且：
  • 设 $k$ 为 $\{a_n\}$ 中最后一个 负数项．
  • 如果 $a_{k + 1} > 0$，则 $\{S_n\}$ 唯一最小项 为 $S_k$．
  • 如果 $a_{k + 1} = 0$，则 $\{S_n\}$ 有 两个最小项 $S_k$，$S_{k + 1}$．
• $a_1 > 0$，$d < 0$：$\{a_n\}$ 先正后负，$\{S_n\}$ 无 最小项，且：
  • 设 $k$ 为 $\{a_n\}$ 中最后一个 正数项．
  • 如果 $a_{k + 1} < 0$，则 $\{S_n\}$ 唯一最大项 为 $S_k$．
  • 如果 $a_{k + 1} = 0$，则 $\{S_n\}$ 有 两个最大项 $S_k$，$S_{k + 1}$．

例题 2.4

已知等差数列 $\{a_n\}$，前缀和 $\{S_n\}$，$a_1 = 9$，$\df {S_9} 9 - \df {S_5} 5 = -4$，求 $\{S_n\}$ 的最大项．

例题 2.4 解答

$$\df{S_9}9 - \df{S_5}5 = \df{9a_5}9 - \df{5a_3}5 = a_5 - a_3 = 2d = -4 \iff d = -2$$

$a_1 = 9$，$d = -2$，求最后一个正数项：$9 - 2(n - 1) = 11 - 2n > 0$，可知 $n < \df {11}2$，即 $n = 5$ 为最后一个正数项，$S_5$ 为一个最大项．

而 $a_6 = -1 \ne 0$，因此 $S_6$ 不是最大项．综上，$\{S_n\}$ 的最大项为第 $5$ 项．

函数视角看等差数列

数列的通项可以视作 定义域为整数 的函数，我们可以将其拓展到 定义域为实数 的情况，用连续函数的知识研究它们，有时有更好的效果．

$$a(n) = a_1 + (n - 1)d = dn + a_1 - d$$

因此 等差数列的通项公式一定符合形态 $An + B$，是一个 一次函数或常函数．

同时，在 $An + B$ 中，对任意 $A, B \in \R$，方程组 $\bcs A = d \\ B = a_1 - d \ecs$ 恒有解 $\bcs a_1 = A + B \\ d = A \ecs$，

因此 通项公式符合形态 $An + B$ 的数列一定是等差数列．

综上，等差数列的通项与 $An + B$ 可以构成双射．

结论不能在答题直接使用

数列 $\{a_n\}$ 的通项公式为一次函数，因此 $\{a_n\}$ 为等差数列．

这个逻辑是 正确的，但在大题中 不能直接使用．

大题中需要按照等差数列证明的方式，证明 $a_{n + 1} - a_n$ 为一常数．

$$S_n = na_1 + \df{n(n - 1)}2 d = \red{\df d 2} \cdot n^2 + \red{(a_1 - \df d 2)} \cdot n$$

建议把上面这个形式记下来，记忆要点：

• 为一个 不超过二次 的 多项式．
• 无常数项．
• 二次项系数为 $\df d 2$，一次项系数为 $a_1 - \df d 2$．

记下来形式之后，已知等差数列的 $a_1$ 与 $d$ 即可很方便地写出 $S_n$．

如已知 $a_1 = 2$，$d = 3$，则 $S_n = \df d 2 \cdot n^2 + (a_1 - \df d 2) \cdot n = \df 3 2 n^2 + \df 1 2 n$．

在大题中 不能直接使用，需要 中间用等差数列求和公式写一步过程，结果用上面的方法计算后直接誊写．

下面开始推性质：

性质零（双射性）：对任意形式满足 $An^2 + Bn$ 的式子（$A, B \in \R$），方程组 $\bcs A = \fr d 2 \\ B = a_1 - \fr d 2 \ecs$ 恒有解 $\bcs a_1 = A + B \\ d = 2A\ecs$，

因此 等差数列的前缀和通项 可以与 $An^2 + Bn$ 构成双射，是一 无常数项 的 不超过二次 的多项式．

性质一：

$d = 0$ 时发生三个退化：等差数列退化为常数列，函数 $a$ 退化为常函数，函数 $S$ 退化为一次函数或常函数．

$d \ne 0$ 时上述三个退化 均不发生，即函数 $S$ 一定是 二次函数，函数 $a$ 一定是 一次函数．

• $\*d > 0$ 时，函数 开口向上．
• $\*d < 0$ 时，函数 开口向下．

反过来，$S(n)$ 的 开口方向 也可以推出 $d$ 的 正负．

性质二：函数 $S$ 常数项为零，可以推出 $\*S(0) = 0$．$S$ 的图像 过原点．

这条性质给出，如果 $S$ 为二次函数（不退化），且对称轴为 $n_S$，则 $S$ 的另一零点一定是 $2n_S$．反过来知道另一零点，其一半就是对称轴横坐标．

因此，性质二 主要给出了 $S$ 的 另一零点 与 $S$ 的 对称轴 的 二倍 关系．

性质三：当 $d \ne 0$（保证不退化），设函数 $S$ 的 最值点 为 $n_S$，函数 $a$ 的 零点 为 $n_A$，我们有

$$n_S = -\df{B}{2A} = \df 1 2 - \df{a_1}d$$ $$a_1 + (n_A - 1)d = 0 \implies n_A = 1 - \df{a_1}d$$

可以发现，$\* n_S = n_A - \df 1 2$，即 $S(n)$ 的最值点（对称轴）恰好相对 $a(n)$ 的零点 左偏 $\* \df 1 2$．

性质三 给出了 $S(n)$ 的最值点与 $a(n)$ 的零点的偏移关系，用来进行 两个函数形态的互推．

例题 2.5.1

设等差数列 $\{a_n\}$ 的前缀和 $\{S_n\}$ 满足 $S_6 > S_7 > S_5$．解不等式：$S_nS_{n + 1} < 0$．

这类条件主要为含 $a_n$ 与 $S_n$ 的 不等式 的题目，基本都是用 确定 $a$ 与 $S$ 函数形态 的方式解决，而解决的工具正是上面讲到的三条性质：

• 性质一：$S$ 开口方向与 $d$ 正负的对应．
• 性质二：$S$ 一定过原点，另一零点与其对称轴的二倍关系．
• 性质三：$S$ 对称轴为 $a$ 零点左偏 $\df 1 2$ 的关系．

除此之外，这个性质也很常用：二次函数中，两点函数值 的 大小关系 与 两点到对称轴的距离 的 大小关系 之间存在对应关系．如开口向上的函数，函数值更小 与 到对称轴距离更近 可以互相等价．

这个性质主要用来根据已知条件 确定对称轴的位置．

例题 2.5.1 解答

$S_5 < S_6 > S_7$，函数先增后减，直接推知 $S(n)$ 为一个最值点位于 $(5, 7)$，开口向下的二次函数．

开口向下，函数值越大距离对称轴越近．

$S_5 < S_7$，可知对称轴与 $n = 5$ 和 $n = 7$ 中距离后者更近，即对称轴位于 $(6, 7)$．

又根据 $S_6 > S_7$，可知对称轴位于 $(6, 6.5)$．

根据 性质二，$S(n)$ 过原点，根据对称性，另一个零点位于 $(12, 13)$，示意图如下：

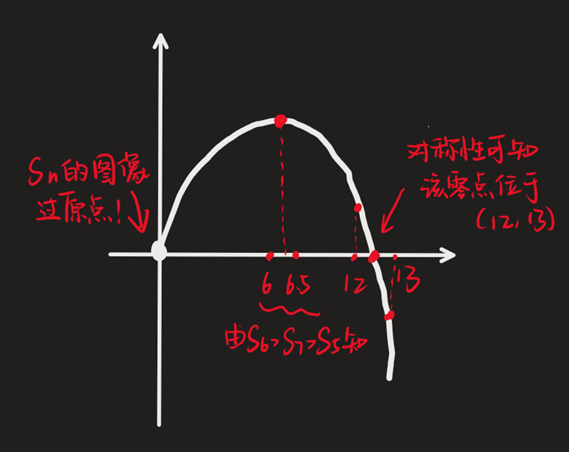
$S_nS_{n + 1} < 0$ 就是在说 $S(n)$ 与 $S(n + 1)$ 异号．观察示意图，很明显可以看出，在 $n$ 为正整数时，当且仅当 $n = 12$ 时 $S(n)$ 与 $S(n + 1)$ 异号，因此本题的答案是 $12$．

本题条件和问题都不含 $a(n)$，因此用来转换 $a$ 零点和 $S$ 最值点的 性质三 没有用到，下面来看一个需要综合考虑 $a(n)$ 与 $S(n)$，在考试中更为常见的题目：

例题 2.5.2

已知等差数列 $\{a_n\}$ 前缀和 $\{S_n\}$，若 $S_{2023} < 0$，$S_{2024} > 0$，下列结论正确的是（ ）【多选】．

• A. $\{a_n\}$ 递增
• B. $|a_{1013}| < |a_{1012}|$
• C. $S_{1012}$ 为 $\{S_n\}$ 的最小项
• D. $S_{1015} > S_{1008}$

例题 2.5.2 解答

首先，$S(n)$ 一定为二次函数（过原点 的一次函数或常零函数不可能满足 $S(2023) < 0$ 且 $S(2024) > 0$）．

绘图．

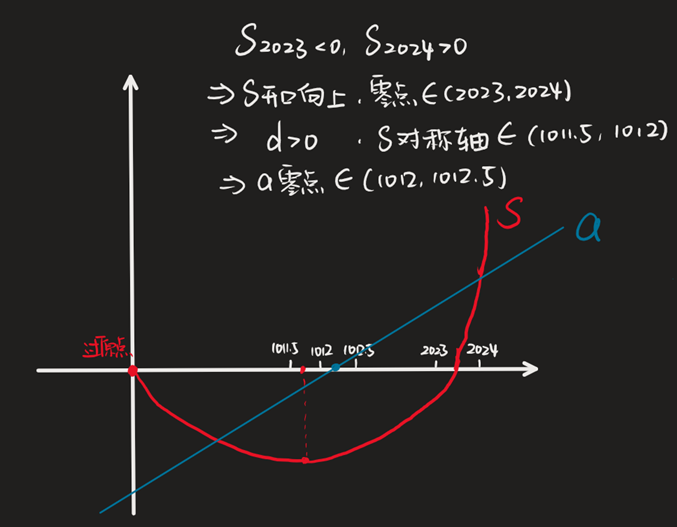
• A. $\{a_n\}$ 递增．显然正确．
• B. $|a_{1013}| < |a_{1012}|$．错误，$1012$ 距离 $\{a_n\}$ 的零点更近，绝对值更小．
• C. $S_{1012}$ 为 $\{S_n\}$ 的最小项．正确，$1012$ 是距离 $\{S_n\}$ 对称轴最近的整点．
• D. $S_{1015} > S_{1008}$．对称轴距离 $1015$ 的距离范围 $(3, 3.5)$，距离 $1008$ 的距离范围 $(3.5, 4)$，$1015$ 距离对称轴更近，函数值更小，错误．

因此选择 AC．

例题 2.5.3

已知等差数列 $\{a_n\}$ 的前缀和 $\{S_n\}$，存在 $m \ne n$ 使得 $S_n = m$ 且 $S_m = n$，则 $S_{m + n} =$（ ）．

• A. $-m$
• B. $-n$
• C. $-(m + n)$
• D. $m + n$

遇到这种 条件只含 $\{S_n\}$，不含 $\{a_n\}$ 的（或 $\{a_n\}$ 条件很容易转成 $\{S_n\}$ 的），可以考虑设函数 $S(n) = An^2 + Bn$ 解决问题．

例题 2.5.3 解答

设 $S(n) = An^2 + Bn$．则

$$S_{m + n} = (m + n)[A(m + n) + B]$$

而条件等价于

$$\begin{cases} An^2 + Bn = m \\ Am^2 + Bm = n \end{cases}$$

结构相似的式子，通常考虑相减（尤其这种轮换对称形成的式子）．

下减上得

$$A(m - n)(m + n) + B(m - n) = -(m - n)$$

由于 $m \ne n$，$m - n \ne 0$，因此

$$A(m + n) + B = -1$$

于是

$$S_{m + n} = (m + n)[A(m + n) + B] = -(m + n)$$

选 C．

等差数列性质的函数推广

事实上，等差数列的性质一、二、四可以写成函数形式，从而将定义域从正整数推广到所有实数．推广形式请勿在大题使用．

下设等差数列 $\{a_n\}$．

性质一函数形式

$$a(n) - a(m) = (n - m)d$$

对任意 $n, m \in \* \R$ 均成立．原因明显．

性质二函数形式

下标守恒定律中，所有下标推广到实数并变成函数自变量，定律仍然成立．因为当时推下标守恒定律的时候，只用到了 $\{a_n\}$ 的通项，并没有用到 $\{a_n\}$ 的离散性．

这也就意味着你可以写出

$$a_2 + a_3 > 0 \iff 2a(2.5) > 0 \iff a(2.5) > 0$$

这种东西．

例题 2.6

已知 $\{S_n\}$ 为等差数列 $\{a_n\}$ 的前缀和，$S_{15} < S_{10}$，且 $a_1 + a_{14} + a_{15} + a_{19} > 0$，求 $\{S_n\}$ 的最大项．

所有条件都是不等式，一般通过画图像解决．但在画图像之前，先用性质理论推出 $d$ 的正负 比较合适（否则画图像需要分类讨论开口方向，比较麻烦）．

例题 2.6 解答

$$S_{15} < S_{10} \iff a_{11} + a_{12} + a_{13} + a_{14} + a_{15} < 0 \iff a_{13} < 0$$$$a_1 + a_{14} + a_{15} + a_{19} > 0 \iff a(12.25) > 0$$

可看出 $\{a_n\}$ 的零点位于 $(12.25, 13)$，且单调递减，$d < 0$．

因此，$\{S_n\}$ 开口向下，对称轴位于 $(11.75, 12.5)$，可看出 $12$ 一定是与对称轴最近的整点，因此答案为 $S_{12}$．

性质四函数形式

$$S(n) = a(\df{n + 1}2)$$

对任意 $n \in \* \R$ 恒成立．直接代入 $\{S_n\}$ 与 $\{a_n\}$ 的解析式即可得证．

例子：$S_{16} > 0$ 可以推出 $a(8.5) > 0$．

首项与公差相等的等差数列

满足 $a_1 = d$ 的等差数列有以下性质：

• 通项公式 $a_n = nd$．同理，任何 正比例函数 作为通项公式恰好对应一个 $a_1 = d$ 的等差数列．
• $a(0) = 0$．
• 对任意数列 $\{a_n\}$，它是 $a_1 = d$ 的等差数列，等价于 对任意 $m, n \in \N^\ast$，$a_{m + n} = a_m + a_n$．

第三条的证明

对任意数列 $\{a_n\}$：

$\{a_n\}$ 是一个满足 $a_1 = d$ 的等差数列，推出 $a_{m + n} = a_m + a_n$：

$$a_{m + n} = (m + n)d = md + nd = a_m + a_n$$

$a_{m + n} = a_m + a_n$ 推出 $\{a_n\}$ 是一个满足 $a_1 = d$ 的等差数列：

对任意 $n \in \N^\ast$，令 $m = 1$，有 $a_{n + 1} = a_1 + a_n$，整理得 $a_{n + 1} - a_n = a_1$．

因此 $\{a_n\}$ 为等差数列，且公差 $d$ 与首项 $a_1$ 相等．